3 zadania z konkursu 05.11.10 Neox: Zadanie 1. Wyznaczyć wszystkie liczby abcde podzielne przez 36, których cyfry spełniają warunki: a<b<c<d<e. Zadanie 2. Dodając sumę, różnicę, iloczyn i iloraz dwóch liczb całkowitych otrzymamy liczbę 450. Znaleźć te liczby. Zadanie 2. Uzasadnij, że w trójkącie prostokątnym suma długości przyprostokątnych jest równa sumie średnic okręgu wpisanego w ten trójkąt i opisanego na tym trójkącie.

Kuba: Ad 1. Liczba jest podzielna przez 36 jeśli jest podzielna przez 4 i przez 9. Z warunku a<b<c<d<e otrzymamy 8>=d>=4 i 9>=e>=5. Z cechy podzielności przez 4 wynika, że liczba de musi być podzielna przez cztery, co zajdzie w przypadku gdy e=8 i (d=4 lub d=6) lub e=6 i d=5. a) e=8 d=4 −> jedyną możliwą liczbą jest 12348 − suma jej cyfr jest podzielna przez 9 więc 12348 jest OK. b) e=8 d=6 −> 8+6=14, reszta z dzielenia 14 przez 9 to 5 tak więc a+b+c musiałoby dać przy dzieleniu przez 9 dać resztę 4, ale a+b+c>=6 (123) i a+b+c<=12 (345), więc ten przypadek odrzucamy. c) e=6 d=5 −> 6+5=11, reszta z dzielenia 11 przez 9 to 2, więc a+b+c musiałoby dać przy dzieleniu przez 9 resztę 7, ponieważ a+b+c>=6 (123) i a+b+c<=9 (234) więc a+b+c=7. Ponieważ c<=4 otrzymujemy jedyną możliwość a=1 b=2 c=4, czyli liczbę 12456. Dostaliśmy dwie możliwe liczby: 12456 i 12348. Ad 2. Oznaczam szukane liczby jako x i y. x+y+x−y+xy+x/y=450 2x+xy+x/y=450 2xy+xy²+x=450y x(y²+2y+1)=450y x(y+1)²=450y x(y+1)²=450y x(y+1)²=2*3²*5²*y Teraz trzeba zauważyć, że NWD(y,y+1)=1, więc musi być y+1=3, lub y+1=5, lub y+1=3*5. Otrzymujemy stąd y=2 wtedy x=100, y=4 wtedy x=72, y=14 wtedy x=28. Tak na szybko więc mogłem coś skrewić, kilkuminutowy relaks przed wyjsciem do domu

Basia: nie zgadzam się a np. y=9 x*100=450*9 x=45*9= 405 całe rozumowanie jest poprawne tylko końcowe wnioski nie całkiem (chyba z pośpiechu, bo skąd np.y+1=4 ?) może być: y+1=2 y+1=3 y+1=5 y+1=6 y+1=10 y+1=9 y+1=15 y+1=25

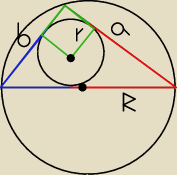
N.: Musimy udowodnić, że 2R+ 2r= a+b Wiemy, że czworokąt zaznaczony na zielono ma 4 kąty proste( jeden trójkąta, dwa− między promieniem a styczną) i dwa odcinki tej samej długości− promienie okręgu wpisanego− jest więc kwadratem. Teraz długość boku a można zapisać jako r+x, a boku b r+y. Jeśli z jednego punktu leżącego na zewnątrz okręgu poprowadzimy dwie styczne, to długości odcinków łączących ten punkt z okręgiem są równe (czerwone i niebieskie). Z tego twierdzenia wynika, że średnica okręgu opisanego na Δ ma długość x+y a+b możemy w takim razie zapisać r+x+r+y= 2r+2R c.k.d.