Udowodnij, że każdy z dwóch odcinków, na które dwusieczna kąta wewnętrznego w tr Marta: Udowodnij, że każdy z dwóch odcinków, na które dwusieczna kąta wewnętrznego w trójkącie dzieli przeciwległy bok, jest krótszy od tego z boków trójkąta, z którym ten odcinek ma wspólny koniec.

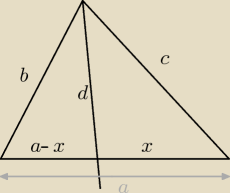
Godzio: Z tw. o dwusiecznej:

b		c
	=
a − x		x

	c(a − x)
xb = c(a − x) ⇒ b =
	x

xb + cx = ca

	ca
x(b + c) = ca ⇒ b + c =
	x

b + c > a

ca
	> a
x

ca >ax /:a c > x Spróbuj podobnie wykazać resztę jak nie dasz rady to pomogę

Marta: skąd wziąłeś xb+cx =ca ?

Godzio: pomnożyłem obustronnie przez (a − x)x

Marta: Dzięki wielkie, poradziłam sobie