UDOWODNIANIE GEOMETRYCZNE Marta: Udowodnij, że każdy z dwóch odcinków, na które dwusieczna kąta wewnętrznego w trójkącie dzieli przeciwległy bok, jest krótszy od tego z boków trójkąta, z którym ten odcinek ma wspólny koniec.

Marta: Ponawiam prośbę

Marta: HELP

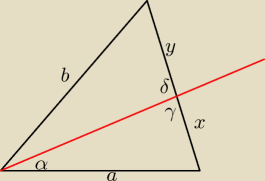
Basia: δ=180−y z tw.sinusów

sinα		sinγ
	=
x		a

a*sinα=x*sinγ

	a*sinα
x=
	sinγ

ponownie z tw.sinusów

sinα		sin(180−γ)
	=
y		b

sinα		sinγ
	=
y		b

b*sinα=y*sinγ

	b*sinα
y=
	sinγ

	a*sinα		b*sinα		(a+b)*sinα
x+y =		+		=
	sinγ		sinγ		sinγ

z warunku trójkąta x+y<a+b stąd:

(a+b)*sinα
	<a+b /:(a+b)
sinγ

sinα
	<1
sinγ

w takim razie

	sinα
x = a*		<a*1<a
	sinγ

	sinα
y = b*		<b*1<b
	sinγ

c.b.d.o.