zbiór wartości funkcji kwadratowej nikka: Zad. 1 Wyznacz zbiór wartości funkcji y = x² + 1 x ∊ <−2,2> Jak najprościej rozwiązać to zadanie?

sushi_ gg6397228: policzyc czy wspolrzedne wierzcholka "p" nalezy do przedzialu <−2,2> jak tak to policz f(−2), f(2) ,q jak nie to policz f(−2) i f(2)

nikka: ok, a co jeśli jeszcze nie zna się wzorów na współrzędne wierzchołka i nie przerabiało funkcji kwadratowej?

sushi_ gg6397228: to trzeba podstawic pare punktow i zrobic wykres

nikka: Sushi wykresu też nie wolno może inaczej − rozwiązanie było następujące: −2 ≤ x ≥ 2 0≤x²≤4 |+1 1≤x²+1≤5 1≤y≤5 nie rozumiem przejścia od pierwszej nierówności do drugiej...

sushi_ gg6397228: −2≤x ≤ 2 jak podniesiesz do kwadratu obustronnie to dostaniesz x² ≤ 4 ( dla tej prawej nierownosci) ale wiesz ze x²≥0 wiec masz 0≤x²≤4

nikka: jest to logiczne, ale dlaczego tylko x ≤ 2 podnosimy do kwadratu? a co z x ≥ −2?

sushi_ gg6397228: wtedy wyjdzie 4≤x²≤4 a do kwadratu mozna podnies wtedy kiedy obie strony so dodatnie x≥−2 to jak sie podniesie do kwadratu to wyjdzie x²≥4 a to głupota (np x=1 1≥−2 ale 1² nie jest ≥ 4)

nikka: ok, rozumiem, że w przedziale <−2, 2> nierówność x² ≥ 4 nie zawsze jest spełniona, więc musimy ją odrzucić , zostaje ta druga i dokładamy x² ≥ 0 bo to jest prawdą dla dowolnego x z naszego przedziału a taki przykład f(x) = −2x² + 3 x∊<−3,2> −3 ≤ x ≤ 2 0 ≤ x² ≤ 9 tu pojawiło się coś takiego i tu dla odmiany 'lewa' nierówność jest podniesiona do kwadratu i zmieniony znak... a tam jest −3 ...

sushi_ gg6397228: no tak ( najlepiej to zrozumiec biorac liczby calkowite z tego przedzialu i podnoszac je do kwadratu)

sushi_ gg6397228: bo jak bedzie −3≤x≤4 0≤x²≤16

nikka: przepraszam pomyłka − powinno być f(x) = −2x² − 3

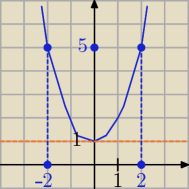
Bogdan: Wykresem funkcji jest parabola y = x² + 1 Zbiór wartości dla x∊<−2, 2> : ZW: y∊<1, 5>

sushi_ gg6397228: to na razie nie ma znaczenia wazne ze jak masz przedzial <−a; b> to 0≤x² ≤ max{a²; b²} ( wypisz liczby dla tego podanego przedzialu <−3,2> tj −3,−2,−1,0,1,2 podnies na kwadratu i zobaczysz co wyjdzie )

think: −3 ≤ x ≤ 2 podnosisz stronami do kwadratu 0 ≤ x² ≤ 9 / *(−2) 0 ≥ −2x² ≥ −18 odejmujesz stronami 3 −3 ≥ −2x² − 3 ≥ −21

Bogdan: Zadanie sprowadza się do wyznaczenia najmniejszej i największej wartość funkcji f(x) = x² + 1 w przedziale <−2, 2>. Odcięta wierzchołka paraboli x_w = 0. f(0) = 1 Obliczamy wartości funkcji na końcach podanego przedziału: f(−2) = 5, f(2) = 5. Najmniejsza wartość jest równa 1, największa 5. Funkcja jest ciągła w przedziale <−2, 2>, a więc zbiór wartości funkcji w tym przedziale ZW = <1, 5>

nikka: ja to wszystko wiem , ale to zadanie ma rozwiązać uczeń pierwszej klasy liceum... Think dlaczego po podniesieniu do kwadratu wyszło Ci 0 ≤ x² ≤ 9 ? ten moment mnie interesuje, dalsze przekształcenia rozumiem.

sushi_ gg6397228: Nikka prosilem CIebie abys wypisala liczby calkowite z tego przedzialu i podniosla je do kwadratu oraz co napisalem o 22.44

nikka: Sushi czyli jeśli x∊<−a,b> to wybieram albo a² albo b² w zależności od tego która liczba będzie większa i wtedy x ≤ od tej liczby czyli tu 9. W pierwszym przykładzie a²=b² = 4 czyli x² ≤ 4.

think: nikka, bo (−2)² = 4 (−1)² = 1 0² = 0 1² = 1 2² = 4 3² = 9 więc jak widzisz x² mieści się między 0 a 9

nikka: chodzi o to, że cokolwiek z tego przedziału podniosę do kwadratu to zawsze będzie ≤ 9

sushi_ gg6397228: a z dołu bedziesz ograniczona przez 0

nikka: uprzedziłeś mnie think generalnie powiedziałabym, że rozpisywanie dziedziny na np. −3≤x≤2 jest niepotrzebne, sprawdzamy jak zachowuje się x² w podanym przedziale i następnie przekształcamy nierówność tak aby w środku uzyskać naszą funkcję... już wszystko wiem − dzięki Wszystkim za pomoc, bo strasznie mnie to nurtowało (a nie można było wykorzystać bardziej zaawansowanych metod)...

sushi_ gg6397228: Think===ONA

nikka: ojej to przepraszam

sushi_ gg6397228: dlatego mi sie wtrąciła

nikka:

think: spokojnie nikka mogłabym być zaniepokojona gdybyś twarzą w twarz się do mnie zwróciła per koleś, a tak to luzik

nikka: uff jeszcze raz dzięki i zmykam spać

think: dobrej nocy