pole trójkąta qwe: Proste zadanie na pole trójkąta: W trójkącie prostokątnym przyprostokątne mają długość 12 cm i 5cm. Przez wierzchołek kąta prostego poprowadzono prostą, która podzieliła ten trójkąt na dwa trójkąty o równych obwodach. Oblicz stosunek długości promieni okręgów wpisanych w powstałe trójkąty.

qwe: refff

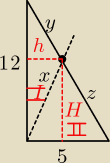
sushi_ gg6397228: zrob rysunek policz 3 bok potem pomysl ile musi wyniesc podzial przeciwprostokatnej na dwie czesci 12+h+x==== 5+h+ y x+y= (przeciwprostokatna)

think: przeciwprostokątna to c² = 12² + 5² ⇒ c = 13 oraz c = y + z mają równe obwody, więc 12 + x + y = 5 + x + z 7 + y = z 13 = y + (7 + y) 2y = 6 y = 3 z = 10 promień okręgu wpisanego w trójkąt to

	2P
r =
	O

h		y
	=		⇒ h = ...
5		c

H		z
	=		⇒ H = ...
12		c

	1
PI =		*12*h
	2

	1
PII =		*5*H
	2

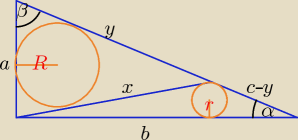Bogdan: L = a + x + y = b + c − y + x ⇒ 2y = b + c − a

	c − a + b		c + a − b		a		b
y =		, c − y =		, sinα =		, sinβ =
	2		2		c		c

Pole trójkąta z okręgiem o promieniu R:

	1		1		c − a + b		b		ab(c − a + b)
PR =		aysinβ =		a*		*		=
	2		2		2		c		4c

Pole trójkąta z okręgiem o promieniu r:

	1		1		c + a − b		a		ab(c + a − b)
Pr =		a(c − y)sinα =		b*		*		=
	2		2		2		c		4c

	PR		ab(c − a + b)     4c
R =		=
	1   L   2		1   L   2

	Pr		ab(c + a − b)     4c
r =		=
	1   L   2		1   L   2

R		c − a + b		y
	=		=
r		c + a − b		c − y

	R		10
a = 5, b = 12, c = 13, y = 10, c − y = 3,		=
	r		3