zadanie
katarzyna: proszę o pomoc czy funkcja y(x)= sqrt(x) (pierwiastek z x) ma pochodną dla x=0? Podaj
interpretację geometryczną.
3 lis 18:08
katarzyna: anybody help me?
3 lis 18:17
katarzyna: pomoże ktoś

3 lis 18:39
katarzyna: pomoże ktoś?
3 lis 23:05
Jack:
narysuj wykres y=√x i spróbuj narysować styczną do wykresu w x=0 albo policz pochodną y=√x
i sprawdź, czy można wstawić x=0.
3 lis 23:06
katarzyna: wstawić można, i wychodzi 0 czyli pochodnej nie ma?
3 lis 23:12
katarzyna: styczna przechodzi przez x=0
3 lis 23:14
Jack:
co to znaczy że wychodzi zero? Na pewno podstawiłaś do POCHODNEJ (a nie f(x)=√x)? Raczej
powiedz, czy ta linia styczna w zerze jest pionowa, pozioma czy pod jakimś innym kątem?
3 lis 23:17
katarzyna: | | 1 | |
pochodna jest równa |
| , także podstawiając tam zero wyjdzie 0, a styczna jest |
| | 2√x | |
nachylona pod katem, przechodząca przez środek układu współ.
3 lis 23:21
Jack:
podchodna jest ok, ale czy na pewno możesz tu wstawić x=0?

3 lis 23:22
katarzyna: a dlaczego by nie?
3 lis 23:23
katarzyna: aha! mianownik nie może byc równy zero!
3 lis 23:24
katarzyna: czyli co, nie ma pochodnej dla x=0 ...
3 lis 23:27
Jack:
no właśnie

Czyli prosta styczna musiałaby mieć współczynnik a=∞, a tego sobie nie życzymy...
Stąd pochodna w zerze funkcji f(x)=
√x nie istnieje.
3 lis 23:27
katarzyna: z tym podaniem interpretacji geometrycznej? mimo ze pochodnej nie ma.
3 lis 23:29
katarzyna: ok, cofam pytanie, cos mi się pochrzaniło, przeciez interpreatcją jest styczna i ten wykres
3 lis 23:33
Jack:
styczna musiałby mieć wspólczynnik a=∞... To znaczy że musiałaby być linią pionową w x=0. Ale
jak wiadomo to już nie będzie funkcja.
3 lis 23:33
katarzyna: ahhh, tak

3 lis 23:34
katarzyna: mam jeszcze jdno pytanie, co do innego zadania, też z pochodnych a by napisać równanie stycznej
do wykresu funkcji
a) f(x)= 2x2 +3x − 1 dla x= −1
b)f(x) e−x2 dla x=0
c) f(x)= ln(x+1) dla x=0
3 lis 23:38
katarzyna: cz wyszło mi dobrze?
a) y=−x
b) brak pochodnej
c)y=x
3 lis 23:40
Jack:
1. policz pochodną
2. znajdz równanie stycznej (y=ax+b). Wykorzystaj do tego fakt, że znasz punkt wspólny dla obu
funkcji
3. wstaw a, b do wzoru na funkcję liniową.
Zerknij tu
https://matematykaszkolna.pl/strona/379.html (choć nie najlepiej to tu wyjasnione)
3 lis 23:40
Jack:
a) punkt wspólny to (−1,−2), f'(x)=4x+3, czyli styczna to y=−x−3
b) ex2 ?
c) funkt wspóny to (0,0) f'(x)=1/(x+1) czyli styczna to y=x
3 lis 23:45
katarzyna: mi wyszło teraz
a) y= −x +1
b) e do −x do 2
C)y=x
3 lis 23:48
katarzyna: w tym b to chyba nie ma pochodnej
3 lis 23:48
Jack:
b) f(x)=e−x2 ?
3 lis 23:50
katarzyna: | | 1 | |
w b pochodna wychodz |
| |
| | 2xex2 | |
3 lis 23:51
katarzyna: tak własnie tak, coś nie chce mi to wyjśc
3 lis 23:51
Jack:
| | −2x | |
a może |
| ?  |
| | ex2 | |
3 lis 23:53
katarzyna: w książce mam przykład funkcji ex2 i rozwiązanie jest f'(x)= 2xex2
3 lis 23:58
katarzyna: także mysłałam, ze to wygląda podobnie.
3 lis 23:58
Jack:
no tak, bo f'(x)=(ex2)'= {pochodna funkcji zewn. razy poch. funkcji wewn.}=ex2 *
(x2)'=2xex2
Dokładnie analogicznie trzeba zrobić z tym z punktu b).
4 lis 00:00
katarzyna: czyli to moje jest dobrze, w takim razie pochodnej nie ma?
4 lis 00:02
Jack:
no jak dobrze? Przyjrzyj się temu jeszcze raz. Z niewiadomych przyczyn do mianownika wpadł Ci
wyraz 2x i zaginął po drodze minus.
4 lis 00:03
katarzyna: zginął, bo mamy to potęgi minusowej czyli daje nam ułamek.
4 lis 00:05
katarzyna: myslałam, że tak na to trzeba spojrzeć
4 lis 00:06
Bogdan:
Cytat: "styczna musiałby mieć współczynnik a=∞... To znaczy że musiałaby być linią pionową
w x=0. Ale jak wiadomo to już nie będzie funkcja.
Styczna jest prostą. Czy styczna musi być wykresem funkcji?
4 lis 00:07
katarzyna: to pytanie chyba nie do mnie?
4 lis 00:09
Bogdan:
Do każdego

4 lis 00:11
katarzyna: jeśli musi, to co wtedy?

4 lis 00:13
Jack:
pochodną w punkcie interpretujemy jako współczynnik kierunkowy stycznej... Dlaczegóż nie
miałaby być linią pionową? Hm... Faktycznie, możliwe że się pospieszyłem − nie będzie funkcją
ale mimo tego będzie styczną
4 lis 00:17
katarzyna: i jakie wnioski z tego?
4 lis 00:19
Bogdan:
Do rozważań o istnieniu pochodnej w punkcie x0 lepiej nie włączać stycznej. Trzeba
raczej przyjrzeć się definicji pochodnej w punkcie x0.
4 lis 00:21
Jack:
ze istnieje styczna w punkcie x=0 choć nie jest funkcją. Będzie prostą pionową czyli ma postać
x=a, a znajdziesz bo znasz punkt styczności (współrzędną x).
4 lis 00:21
Jack:
nie nie, wszystko jest ok, trzeba tylko wiedzieć, że styczna nie musi być funkcją i będzie w
porządku.
4 lis 00:22
katarzyna: czy to zmienia postać rzeczy tzn. rozwiązania.
4 lis 00:25
Jack:
w tym przykładzie y=√x okazuje się że istnieje pochodna.
4 lis 00:26
Jack:
istnieje styczna, sorry.
4 lis 00:26
katarzyna: czyli istnieje interpretacja geometryczna?
4 lis 00:28
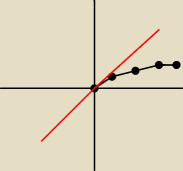
katarzyna:
4 lis 00:31
Jack:
nie no, interpertacja geometryczna istnieje (tzn. da się ją przeprowadzić). Popełniłem błąd
pisząc że styczna nie istnieje. Po prostu nie jest ona funkcją, jest linią pionową.
4 lis 00:31
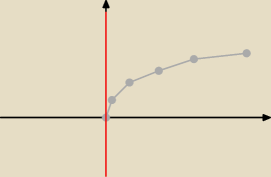
Jack:
4 lis 00:32
katarzyna:
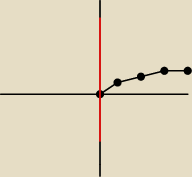
tak?
4 lis 00:33
Jack:
o właśnie.
4 lis 00:34
katarzyna: a dlaczego nie tak jak wcześniej narysowałam?
4 lis 00:34
Jack:
bo wartość pochodnej w zerze wyszła nam ∞. Czyli linia musi być pionowa. Gdyby była jakkolwiek
inaczej nachylona wówczas z pochodnej wyszłaby jakaś liczba.
4 lis 00:36
katarzyna: właśnie nie rozumiem jak wyszło ∞?
4 lis 00:38
katarzyna: przepraszam, ze tak cięzko to mi idzie, ale ja dopiero się z tym zaznajamiam
4 lis 00:40
Jack:
| | 1 | | 1 | |
wyszło f'(x)= |
| . Teraz jak wstawisz do mianownika 0, wyjdzie |
| =∞. |
| | 2√x | | 0 | |
4 lis 00:41
katarzyna: | | 1 | | 1 | |
wartość pochodnej wychodzi nam |
| bp f'(x)= |
| |
| | 0 | | 2√x | |
4 lis 00:42
katarzyna: ahaaaa
jejciu soryy, zapomniałam całkiem o tym.
4 lis 00:42
katarzyna: az tym przykładem b, to jak w końcu będzie?
4 lis 00:48
Jack:
tak jak napisałem, styczna też wyjdzie i będzie nawet funkcją

4 lis 00:49
4 lis 00:52
katarzyna: ?
4 lis 00:52
katarzyna: wyszło mi y= −x
4 lis 01:02
Jack:
tak, tak będzie wyglądała. albo inny zapis: −2x*e−x2
4 lis 01:02
Jack:
w jakim punkcie liczysz pochodną?
4 lis 01:03
katarzyna: dobrze?
4 lis 01:03
katarzyna: x=0
4 lis 01:04
Jack:
dobrze, liczysz dla x=0. Czyli ile wychodzi f'(0)? (przepraszam za te pytania...)
4 lis 01:08
katarzyna: wychodzi zero, czyli co ? nie ma pochodnej, bo ja juz się gubię.
4 lis 01:10
Jack:
pochodna wychodzi nam 0, a pochodna funkcji w punkcie to współczynnik "a" stycznej. Czyli nasza
styczna ma postać y=0x+b czyli y=b. Trzeba teraz znaleźć "b". W tym celu znajdź wartość
współrzędnej "y" w punkcie w którym liczysz pochodną (podstaw ten punkt do funkcji pierwotnej
i wylicz "y").
Wcześniej wychodziło ∞ dlatego mieliśmy małe zatrzęsienie.
4 lis 01:14
katarzyna: oooo matko, za dużo informacji o tej godzinie

czyli co? y=0
4 lis 01:18
Jack:
f(x)=e−x2
Liczymy f(0)=e0=1
Wiec nasz punkt w którym liczymy styczną to (0,1) Stąd wynika że współrzędna y=1
Czyli nasza styczna, skoro przechodzi tez przez ten punkt, ma postać y=1.
4 lis 01:23
Jack: uciekam, powodzenia dalej!

4 lis 01:25
katarzyna: dzięki, ja podstawiłam pod wzór pochodnej,i dlatego to wyszło,
już trochę nie kontaktuję
4 lis 01:25


 Czyli prosta styczna musiałaby mieć współczynnik a=∞, a tego sobie nie życzymy...
Stąd pochodna w zerze funkcji f(x)=√x nie istnieje.
Czyli prosta styczna musiałaby mieć współczynnik a=∞, a tego sobie nie życzymy...
Stąd pochodna w zerze funkcji f(x)=√x nie istnieje.






 tak?
tak?

 czyli co? y=0
czyli co? y=0
