trygonometria
Enio: Pomoże ktoś?
2 lis 20:55
Grześ: Na jedną stronę wg mnie trzeba a w między czasie dla szybszego pisania:
Oraz dziedzinę określ
sin2x=t t∊<−1,1>
2 lis 21:01
sushi_ gg6397228:
sin 2x= t zalozenie −1≤t≤1
i potem leciasz jak dla zwyklego wielomianu, na jedna strone, wspolny ułamek
2 lis 21:04
Grześ: a co ja zrobiłem sushi
troszkę mu pomogłem
2 lis 21:05
sushi_ gg6397228:
nie kliknalem odświez i dlatego nie mialem widoku co napisali poprzednicy
2 lis 21:09
Grześ: spoko, teraz ma juz z górki, jeśli ja byczka nie zrobiłęm, jak coś sushi, to prześledź
obliczenia
2 lis 21:10
Enio: a tam będzie założenie że 1−t2 różne od zera?
2 lis 21:56
Enio: 1−t2≠0
t≠1 i t≠−1
(2t2+3t−2)(1−t2)≤0
Δ=9+16
√Δ=5
t1=−2 −−− nie spełnia założenia
t2=12
2 lis 22:20
sushi_ gg6397228:
| | 1 | |
t1=1, t2=−1, t3= −2; t4= |
| |
| | 2 | |
robimy fale i pamietamy na koncu o zalozeniu t ∊(−1,1)
2 lis 22:22
Enio:
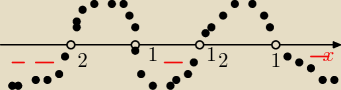
x∊(−
∞;−2)U(−1;
12)U(1;
∞)
2 lis 22:33
Grześ: a to czasem nie jest dla t dziedzina
2 lis 22:34
Grześ: zauważ, że podstawione t∊<−1,1>
2 lis 22:34
Enio: no tak czyli x∊(−1;12>
2 lis 22:37
sushi_ gg6397228:
| | 1 | |
−1<sin x ≤ |
| wiec x ∊ ... pamietaj o okresie |
| | 2 | |
2 lis 22:38
sushi_ gg6397228:
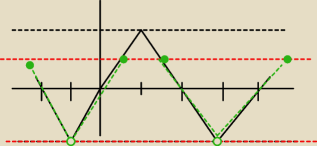
kolor czerwony y=1/2 i y=−1
kolor zielony rozwiazanie
2 lis 23:03
Enio: x∊<π4+2kπ;32π+2kπ)U(32π+2kπ;136π+2kπ>
2 lis 23:12
sushi_ gg6397228:
| | π | |
dalej oszukujesz skad masz |
| |
| | 4 | |
sin 30= 1/2
sin 150= 1/2
x ∊ (− 90 stopni + 2k π; 30 stopni + 2kπ> ∪ < 150 stopni + 2k π; 270 stopni + 2kπ)
2 lis 23:16