Długość promienia okręgu opisanego na trójkącie
aga: Dane są długości boków trójkąta równoramiennego: 25 cm 25 cm 14 cm
Sprawdź, czy dany trójkąt jest ostrokątny, rozwartokątny czy prostokątny.
Oblicz długość promienia okręgu opisanego na tym trójkącie.
1 lis 23:18
kinga: jeżeli a
2+b
2<c
2 to trójkąt jest rozwartokątny
jeżeli a
2+b
2>c
2 to trójkąt jest ostrokątny
jeżeli a
2+b
2=c
2 to trójkąt jest prostokątny
taka podpowiedź
1 lis 23:23
aga: To wiem, bardziej chodzi mi jak obliczyć tutaj R. Wyszło mi 16 lecz nie jestem tego na 100%
pewna...
2 lis 00:07
Bogdan:
Najpierw obliczamy pole trójkąta P wzorem Herona.
| | 25 + 25 + 14 | |
p = |
| = 32, p − 25 = 7, p − 14 = 18 |
| | 2 | |
P =
√32 * 7 * 7 * 18 =
√16 * 2 * 49 * 2 * 9 = 4 * 2 * 7 * 3 = 168
| | abc | | 25*25*14 | |
R = |
| = |
| |
| | 4P | | 4*168 | |
2 lis 00:14
Bogdan:
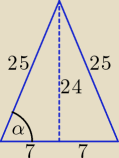
Inny sposób.
Z twierdzenia Pitagorasa obliczamy wysokość opadającą na bok długości 14.
h = 24
| | 25 | |
Z twierdzenia sinusów: R = |
| |
| | 2sinα | |
2 lis 00:23
aga: Dzięki wielkie.
A jest na to jakiś inny sposób? Herona nigdy nie miałam w szkole.
2 lis 00:23
aga: Twierdzenia sinusów też nigdy nie miałam
2 lis 00:25
Bogdan:
Wzór Herona jest jednym z elementarnych wzorów na obliczanie pola trójkata
i powinien być omawiany już w gimnazjum, stosujemy go wtedy, gdy znamy tylko
długości boków trójkąta: a, b, c.
Pole P =
√ p * (p − a) * (p − b) * (p − c)
2 lis 00:27
aga: Super! Dzięki
2 lis 00:34
Bogdan:
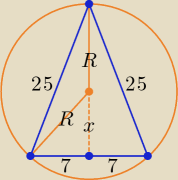
Trzeci sposób:
R + x =
√252 − 72 ⇒ x = 24 − R ⇒ x
2 = 576 − 48R + R
2
| | 625 | |
x2 + 72 = R2 ⇒ 576 − 48R + R2 + 49 = R2 ⇒ 48R = 625 ⇒ R = |
| |
| | 48 | |
2 lis 00:41
oszini: βyyyy
26 wrz 19:07