Wielomiany vir: Wykaż, że wielomian W przybiera wartości dodatnie dla każdego x ∊ R (x−1)(x−3)(x−7)(x−9) + 40 = W(x)

vir: Proszę pomóżcie

vir: jak to robić? może tak: (x² − 4x −3)(x² − 16x − 63) + 40 ale co dalej

vir: nie mam zielonego pojęcia,,, ktoś pomoże?

dziuba: (x²−4x+3)(x²−16x+63)+40 musisz to dalej wymnożyć

Godzio: Jesteś w Liceum czy wyżej vir ?

vir: a jakie to ma znaczenie? wyżej...

Godzio: No tu akurat ma bo tu można myśleć i myśleć sposobami licealnymi a tak mamy pochodne i extrema, można zbadać gdzie funkcja rośnie dokąd rośnie i gdzie maleje, jeśli się zbada to to okaże że nigdy nie przyjmuje wartości ujemnych Pokazać jak czy próbujesz ?

vir: pochodnych jeszcze nie miałem

vir: chociaż te 12 wzorów to umiem bo na fizykę były potrzebne

Godzio: hmmm to w takim razie trzeba pomyśleć nad innym sposobem

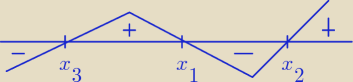
Godzio: Może Ci się przyda, bo inny sposób nie przychodzi mi do głowy W(x) = x⁴ − 20x³ + 130x² − 300x + 229 W'(x) = 4x³ − 60x² + 260x − 300 W'(x) > 0 4x³ − 60x² + 260x − 300 > 0 /: 4 x³ − 15x² + 65x − 75 > 0 −−− z tw. o pierwiastkach wymiernych rozkładasz sobie to wyrażenie: (x − 5)(x − √10 − 5)(x + √10 − 5) > 0 x₁ = 5 , x₂ = √10 + 5, x₃ = −√10 + 5 W(5) = 104 W(√10 + 5) = 4 W(−√10 + 5) = 4 Jak widać po ekstremach gdybyś naszkicował wykres to okaże się że funkcja jest cała dodatnia Co do wartości √10 + 5 i −√10 + 5 podstawiłem do równania które dałeś na samym początku i w miarę ładnie się liczyło

Kuba: Najpierw narysuj sobie wykres wielomianu pomijając tą 40−stkę na końcu, a potem ją dodaj do funkcji wielomianowej (jak wiesz wykres przesuwa się wtedy o 40 w górę, bo 40 jest dodawane do całej funkcji). Teraz wystarczy tylko sprawdzić czy najmniejsze wartosci wielomianu, tj przyjmowane dla x = 2 i x = 8 nie mają wartości mniejszych od (−40), ale tak nie jest, więc cały wykres po przesunięciu w góre będzie leżał powyżej osi 0x.