 Wykaż ze jeżeli P(B|A)=P(B|A') i P(A)>0 oraz P(A')>0 to zdarzenia A i B są niezależne.
Wykaż ze jeżeli P(B|A)=P(B|A') i P(A)>0 oraz P(A')>0 to zdarzenia A i B są niezależne.
| P(A∩B) | ||
P(B|A) = | ||
| P(A) |
| P(A'∩B) | P(B) − P(A∩B) | |||
P(B|A') = | = | |||
| P(A') | 1 − P(A) |
| P(A∩B) | P(B) − P(A∩B) | ||
= | |||
| P(A) | 1 − P(A) |

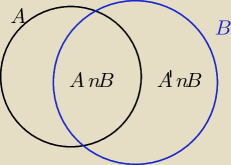
| P(A∩B) | ||
P(B | A)= | ||
| P(A) |
| P(A'∩B) | ||
P(B | A')= | ||
| P(A') |

