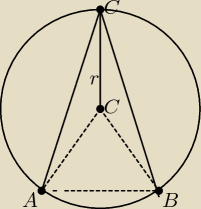
Oblicz pole trójkąta ABC. majka: Z punktu C leżącego na okręgu o promieniu r =10 poprowadzono dwie cięciwy CA i CB równej długości.Kąt ACB ma miarę α = 30*. Oblicz pole trójkąta ABC. Prosze bardzo o rozwiązanie krok po kroku bo jestem zupełnym laikiem z matmy...

majka: BŁAGAM NIECH MI KTOŚ ROZWIĄŻE TO ZADANIE

Bogdan: Jaką miarę ma kąt ACB ?

Bogdan: Oczekuję odpowiedzi od majki, proszę inne osoby o nie podpowiadanie.

Jack:

Bogdan: Który punkt jest C? na okręgu czy w jego środku?

majka: no właśnie sorki zrobiłam błąd na rysunku...oczywiście środek okręgu to O a punkt C leży na okręgu...odpowiadając Bogdanowi to kąt ACB ma 30* natomiast kąt AOB 60*

Bogdan: Ok. Jakim trójkątem jest trójkąt ABO ?

majka: równobocznym jego boki wynoszą podobnie jak promień okręgu 10 a kąty mają miarę 30*

Bogdan: Wszystkie kąty wewnętrzne w trójkącie równobocznym maja miary 60^o. Wiemy więc, że |AB| = 10, ale ta informacja jest zbędna do wyznaczenia pola trójkąta ABC. Trójkąt ABC jest podzielony na 3 trójkąty: ABO − ramiona mają długość 10, kąt AOB między nimi ma miarę 60^o; AOC i BOC − ramiona tych trójkątów mają długość 10, kąt AOC i kąt BOC mają miary po 150^o. Skorzystamy z wzoru na pole trójkąta:

	1
P =		(długość boku) * (długość boku) * sin(miara kąta między tymi bokami)
	2

	1		1
W tym przypadku: P =		r2sin60o + 2*		r2sin150o
	2		2

think: jaką miarę mają kąty w ABO?

majka: kurde znów błąd... kąty w trójkącie AOB mają 60 st

Bogdan: think − prosiłem o nie podpowiadanie

think: Ale ja nie podpowiedziałam podałeś wzór na pole zobaczyłam coś innego więc zaproponowałam to przepraszam nie chciałam popsuć.

Bogdan: majka − kontynuujemy. Ile wynosi sin60^o i sin150^o ?

majka: sin60* √3/2 lub 0.8660 a sin 150* to wstyd się przyznać ale nie wiem

majka: dla mnie matematyka to zawsze była czarna magia i chyba już tak zostanie...

Bogdan:

	3
sin60o =		, nie zamieniamy na wartość przybliżoną.
	2

	1
sin150o = sin(180o − 30o) = sin30o =
	2

Masz teraz wszystkie dane liczbowe do obliczenia pola trójkąta ABC. Podaj ten wynik.

Bogdan: i więcej wiary w siebie

Bogdan:

	√3
poprawiam − sin60o =
	2

majka: nie można wierzyć w siebie jak sprawiają problemy obliczenia teoretycznie proste...aż boje się podać wynik...

majka: ale zaryzykuje...czy to jest 126?

Bogdan: Nie, to nie jest dobry wynik. Podaj w takim razie swoje obliczenia, poszukamy błędu.

majka: no tak pewnie źle obliczyłam...przeliczyłam jeszcze raz i mam nadzieję, że tym razem zrobiłam to dobrze...175?

Bogdan:

	1		1
P =		*r*r*sin60o + 2*		*r*r*sin150o
	2		2

Teraz spróbuj

majka: eh...żal mi siebie jak można być tak tępym...125?

Bogdan: Jeszcze raz.

	1		√3		1		1
P =		*10*10*		+ 2*		*10*10*		= .... dokończ
	2		2		2		2

majka: Dzięki Bogdan, że poświęciłeś mi swój czas chyle czoła przed twą wiedzą ja niestety się poddaję...w moim przypadku jedynym rozsądnym wyjściem jest rezygnacja z matury Pozdrawiam i jeszcze raz dziękuję

Bogdan: dokończę więc, P = 25√3 + 50 i już

think: no to możemy teraz moim sposobem

think: wysokość tego trójkąta równoramiennego h_ABC = h_ABO + r

	a√3		10√3
hABC =		+ r =		+ 10 = 5√3 + 10
	2		2

	1
PABC =		*|AB|*hABC
	2

Bogdan: A czy Twój think sposób jest prostszy i ma mniej przekształceń? W przedstawionym tu rozwiązaniu wystarczyło wyznaczyć miary kątów środkowych: 60^o, 150^o, 150^o i sinusy tych kątów.

majka: No tak ja to sobie lubie życie komplikować....kombinowałam z tym rozwiązaniem jak koń pod górę i nie widziałam tego logicznego...dzięki

think: nie mówię że jest prostszy ale zawsze to jakaś druga opcja

majka: think czy w twoim sposobie obliczenia wynik wynosi 25√3 + 10?

think:

1		1
	(5√3 + 10)*10 =		*10*(5√3 + 10) = 5*(5√3 + 10) = 5*5√3 + 5*10 = 25√3 +
2		2

50 inna odpowiedź przecież nie może być...