wyznacz dziedzine funkcji Anusia1919:

	√8−2x
f(x)=		+1−5xex
	x2−4

Anusia1919: Pomocy:(

roman: chwila ....

Godzio: Anusia gdzie ty się uczyłaś jeśli nie umiesz obliczać dziedziny ?

roman: D: x² −4 = 0 ( x+2)(x−2)=0 i z tego mamy ... x jeden = −2 x dwa = 2 x²−4 większe lub równe od zera i rysujesz parabolę [ mam nadzieje ze wiesz jak ] ( od −2 do 2 pamiętaj a jest dodatnie wiec ramiona do gory ) i dalej ( − nieskończoności ; −2 > u < 2 ; + nieskończoności ) ostatecznie D: (− nieskoń.; −2) u (+2; + nieskoń.) i rysunek z otwartymi kółeczkami [ rysujesz taka długa linie i tam nanosisz x jeden i x dwa] MAM NADZIEJE ZE MNIE ZROZUMIAŁAŚ [ NIE JESTEM DOBRY BY COŚ WYTŁUMACZYĆ ] CHYBA DOBRZE

roman: sorry to jest źle sorry ....

Godzio: 8 − 2x ≥ 0 ⇒ x ≤ 4 i x² − 4 ≠ 0 ⇒ x ≠ 2, x ≠ −2 D = (−∞,−2)∪(−2,2)∪(2,4>

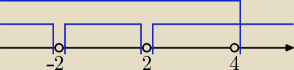
Bogdan: Założenia: 1. x² − 4 ≠ 0 ⇒ (x − 2)(x + 2) ≠ 0 ⇒ x ≠ 2 i x ≠ −2 2. 8 − 2x ≥ 0 ⇒ 2x ≤ 8 ⇒ x ≤ 4 Dziedzina: D_f: x ∊ (−∞, −2)∪(−2, 2)∪(2, 4>

Anusia1919: bo nie wiem co to to e jest co trzeba z takim czymś zrobić !1 i temu nei wiem

Basia: e^x to coś takiego jak 2^x e^x jest liczbą niewymierną 2<e<3 czyli e^x jest stale dodatnie

Basia: poprawka druga linijka nie e^x tylko e

Anusia1919: czyli tego nei bierzemy pod uwage w obliczaniu dziedziny?

Anusia1919: ^1−5x_e^x tego nie rozwiązujemy zeby dziedzine obliczyć tak

Jack: rozwiązujemy, ale wychodzi nam że mianownik nigdy się nie zeruje, wiec niczego nie wyrzucamy z dziedziny.