Funkcja z parametrem i ciąg arytmetyczny Jagoda18: Dane jest równanie: x⁴−10x²+m=0. Wyznacz te wartości parametru m, dla których to równanie ma cztery pierwiastki, z których można utworzyć ciąg arytmetyczny.

Grześ: Zwiń do równania kwadratowego t=x² t≥0 ( czy t>0 )

Jagoda18: Rozwiązałam to. Ogólnie, aby równanie miało 4 pierwiastki to t musi należeć do zbioru (0,25), ale nie wiem co dalej.

Grześ: Teraz trzeba rozpatrzyć, że ułożą ciąg arytmetyczny, nie myslałem nad tym, ale coś z postaci x₁ i x₂ coś pokombinowac trzeba

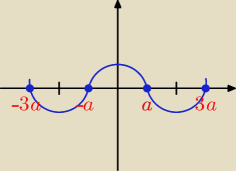
Bogdan: Jeśli wielomian W(x) = x⁴ + bx² + c ma 4 miejsca zerowe, to układają się one symetrycznie względem osi y. Dodatkowo w tym zadaniu odległość między nimi jest stała. Przyjmujemy więc: x₁ = −3a, x₂ = −a, x₃ = a, x₄ = 3a. Tworzymy postać iloczynową wielomianu: W(x) = (x + 3a)(x + a)(x − a)(x − 3a) W(x) = (x² − 9a²)(x² − a²) ⇒ W(x) = x² − 10a² + 9a⁴ Wiemy, że W(x) = x⁴ − 10x² + m, 10a² = 10 ⇒ a² = 1 oraz a⁴ = 1 m = 9a⁴ = 9

Jagoda18: Bardzo dziękuję Bogdan Taką pomoc najbardziej lubię

Bogdan:

matroz: witam, jestem świadomy tego, że odświeżam stare posty; chciałbym, byście rzucili okiem na to zadanie. Wiem już jak je rozwiązać; sam rozwiązałem je w inny sposób, który wymagał mnożenia 4 nawiasów − w jednym dwa, w trzech po trzy składniki. Było w cholerę liczenia (po wymnożeniu wychodzi 54 składniki, które musiałem uporządkować itd.) i na maturze na pewno nie liczyłbym tego, tylko zrezygnowałbym ze względu na czas. Nie chodzi mi o to, by przedstawiać swój sposób rozwiązania − chciałbym tylko byście podpowiedzieli mi, jak wpaść na to, że "Jeśli wielomian W(x) = x⁴ + bx² + c ma 4 miejsca zerowe, to układają się one symetrycznie względem osi y." czy jest na to jakieś prawo matematyczne? Ja na to nie wpadłem więc zadanie sobie zrobiłem sposobem którym zaliczyłem się prawie na śmierć proszę o sugestie, przydadzą mi się, jutro zaczynam robić zadania z funkcji właśnie pozdrawiam

Mila: Do Matroz−a t₁>0 i t₂>0 x1 = √t1 lub x2 = −√t1 lub x3 = √t₂ lub x4 = −√t₂ te liczby są parami symetryczne względem OY

matroz: dziękuję

Mila: Do Matroza Uszereguj pierwiastki na osi, Oblicz r z definicji ciągu. otrzymasz t2 =9 t1 podstaw do wzorów Viet"a otrzymasz t1=9 stąd m=9 (znów z iloczynu pierwiastkow). Nie każdy zauważy te równe odleglości.

matroz: Milo: chyba teraz zbyt skrótowo mi napisałaś, nie zrozumiałem wszystkiego obliczając r, będzie wynosić r=√t₁−√t₂ lub r=√t₂−√t₁ "otrzymasz t2 =9 t1 " −−−−> jak z wzorów Viete'a otrzymam x₁+x₂=5 x₁*x₂=m ale co mi to da Mam kolejny jednak problem z tym zadaniem, kolega Bogdan stwierdził: "Przyjmujemy więc: x1 = −3a, x2 = −a, x3 = a, x4 = 3a. " dlaczego akurat takie wartości (−3,−1,1,3), z czego to wynikło? Muszę to wiedzieć, by ogarnąć to zadanie, jeśli przyjmę inne wartości, nie skończę zadania.

ZKS: Pierwiastki oznaczamy −√t₁ , −√t₂ , √t₂ , √t₁. A z własności ciągu otrzymujemy równanie: −2√t₂ = −√t₁ + √t₂ −3√t₂ = −√t₁ 3√t₂ = √t₁ / ² 9t₂ = t₁. Oczywiście jeszcze w zadaniu trzeba sprawdzić czy dla m = 0 nie mam ciągu arytmetycznego a co się później okaże że dla m = 0 również mamy pierwiastki które tworzą ciąg.

matroz: "dla m = 0 również mamy pierwiastki które tworzą ciąg." w odpowiedziach jest tylko m=9 nie wiem skąd Ci wyszła Twoja równość, ja to zrobiłem tak: √t₁−√t₂=√t₂+√t₂ √t₁=3√t₂ /² t₁=9t₂ wyszło to samo w każdym razie Dzięki!

Mila: Zgadza się. ZKS podał szczegóły. Błąd w sumie pierwiastków!

ZKS: Moja równość wynikała z 2a_n = a_{n − 1} + a_{n + 1}. Widocznie musisz mieć nie pełną odpowiedź jak tak bo dla m = 0 również mamy pierwiastki tworzące ciąg. Dla m = 0 równanie przybiera postać: x⁴ − 10x² = 0 x²(x² − 10) = 0 (x + √10)x²(x − √10) = 0 Stąd dostajemy pierwiastki −√10 , 0 , √10 które tworzą ciąg arytmetyczny o różnicy równej √10.

Mila: A może ciąg ma mieć 4 wyrazy?

ZKS: A czemu nie? Ciąg tworzą dwie liczby.

Aga: ciąg arytmetyczny, czy geometryczny jest co najmniej trzy wyrazowy. Z treści zadania wynika, że trzeba znaleźć m ,dla którego istnieją 4 pierwiastki, z których można ułożyć ciąg arytmetyczny, nie jest napisane, że mają być różne.

k4cp4: @matroz: ja bym powiedział tak: W(x) = W(−x) ⇒ jest to f−kcja parzysta, więc jej pierwiastki (o ile istnieją) są symetryczne względem osi OY, nieważne, czy jest ich 1, 2, 3 czy 4.