sześcian fred: Przekątna sześcianu jest o 2 większa od przekątnej ściany sześcianu. Wówczas krawędź sześcianu jest równa?

Grześ: przekątna: d=a√3 a√3=a+2 3a²=a²+2a+4 2a²−2a−4=0 a²−a−2=0 Δ=1+8=9 √Δ=3

	1+3
x1=		=2
	2

	1−3
x2=		=−1
	2

Krawędź ta wynosi 2

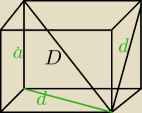
mi: D=d+2 d=a√2 mamy tr. prostokątny a²+d²=D² a²+(a√2)²=(a√2+2)²

Grześ: Machłem się w obliczeniach

Grześ: 2a²−4a−4=0 x²−2a−2=0 Δ=4+8=12 √Δ=2√3

	2+2√3
x1=		=1+√3
	2

	2−2√3
x2=		=1−√3
	2

Krawędź ta wynosi 1+√3

Godzio: Co wy z tymi kwadratami, to zadanie jest prawdopodobnie z gimnazjum a tam równań kwadratowych nie robią a√3 = a + 2 a√3 − a = 2 a(√3 − 1) = 2

	2		√3 + 1		2√3 + 2		2√3 + 2
a =		*		=		=		= √3 + 1
	√3 − 1		√3 + 1		3 − 1		2

Grześ: W sumie racja.

Eta: Godzio popraw: a√3= a√2+2

Bogdan: Ten rysunek mi nie przedstawia sześcianu. Tak jak trzeba dbać o poprawność obliczeń, tak samo trzeba dbać o poprawność załączonych szkiców.

fred: To jest zadanie maturalne

mi: ale czemu a√3=a+2 przecież przekątna sześcianu jest o 2 większa od przekątnej ściany

Godzio: nie doczytałem polecenia ale już wiadomo

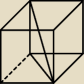
mi: czy teraz lepiej?

Grześ: Haha, więc będzie: a√3=a√2+2 a√3−a√2=2 a(√3−√2)=2

	2		2(√3+√2)
a=		=		=2(√3+√2)
	√3−√2		3−2

Eta:

Bogdan: mi − nie jest lepiej, jeśli stosujesz linie przerywana dla niewidocznych krawędzi, to bądź konsekwentny.

Eta: