Funkcja kwadratowa f przyjmuje największą wartość równą 315 Ola: Funkcja kwadratowa f przyjmuje największą wartość równą 3¹₅, a zbiorem rozwiązań nierówności f(x)>0 jest przedział (−5,3). Wyznacz zwór funkcji f w postaci ogólnej

mi: wykorzystaj wzór na postac iloczynową y=a(x−x₁)(x−x₂) y=a(x−3)(x+5)

	1
wykorzystaj, że dla x=−1 funkcja przyjmuje wartość 3		i oblicz a , potem doprowadź do
	5

postaci ogólnej

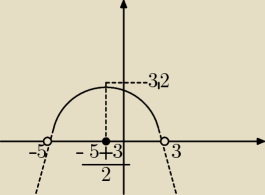
think: jest to funkcja postaci: f(x) = a(x + 5)(x − 3) taka, że należy do niej punkt (−1; 3,2) f(−1) = 3,2 a(−1 + 5)(−1 − 3) = 3,2

	3,2
a =		= −0,2
	4*(−4)

f(x) = −0,2(x + 5)(x − 3) = −0,2(x² + 2x − 15) = −0,2x² − 0,4x + 3

waldek: √16