z góry dziękuję za pomoc Ania: Rozwiaz rownanie: x³+1/x{3}=6(x+1/x) rozwiaz nierownosc: |1/x+2|≤|2/x−1| w nierówności jest znak jest mniejsze od zamiast jest mniejsze lub rowne.

think: zapisz to porządnie... po prawej masz link <Kliknij po więcej przykładów> dowiesz się wtedy jak zapisać ułamki i co tam potrzeba... a jak to zapiszesz już ładnie to i pewnie znajdzie się osoba, która pomoże Ci w Twoim zadaniu.

think: bleh po lewej nie po prawej...

Ania: Rozwiaz rownanie: x³+¹_x{3=6(x+¹_x) rozwiąż nierówność: |¹_x+2|≤|²_x−1|

think: i co tam jest w tym mianowniku? x³

Ania: tak

think: no to już...

	1		1
x3 +		= 6(x +		)
	x3		x

dziedzina: x ≠ 0

x6 + 1		x2 + 1
	= 6*		/ *x3
x3		x

x⁶ + 1 = 6(x² + 1)x² podstawienie t = x² ⇒ t ≥ 0 t³ + 1 = 6t² + 6t (t + 1)(t² − t + 1) − 6t(t + 1) = 0 (t + 1)(t² − 7t + 1) = 0 ⇔ t = −1 odpada bo t ≥ 0 lub t² − 7t + 1 = 0 tutaj liczysz Δ i pierwiastki i pamiętaj że odpowiedzią mogą być tylko t nieujemne...

think:

	1		2
teraz to drugie...|		| ≤|		|
	x + 2		x − 1

dziedzina: x + 2 ≠ 0 i x − 1 ≠ 0 ⇒ x ∊ ℛ \{−2,1}

1		2
	≤
|x + 2|		|x − 1|

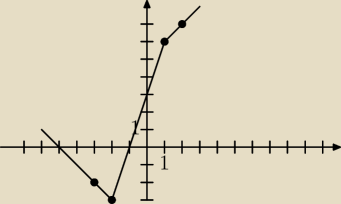
ponieważ wyrażenie w mianowniku jest dodatnie to możemy pomnożyć na krzyż |x − 1| ≤ 2|x + 2| f(x) = 2|x + 2| − |x − 1| i f(x) ≥ 0 f(−3) = 2 − 4 = −2 f(−2) = −3 f(1) = 6 f(2) = 8 − 1 = 7 także ta nierówność jest prawdziwa dla x∊(−∞,−5> ∪<−1,1) ∪ (1,∞)

pancer: x−2y>0

Ania: dziękuję

think: proszę