trapez lipa: w trapezie równoramiennym wysokość ma 16 cm, przekątne są do siebie prostopadłe, a ich punkt wspólny dzieli każdą z nich na odcinki, których stosunek wynosi 3:5. oblicz obwód trapezu

Olex:

	90
α=		=45
	2

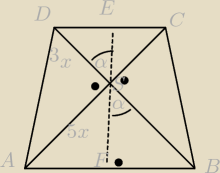
	IFSI		√2		5x		5√2
cosα=		=		ISFI=		=
	IBSI		2		√2		2

	IESI		√2		3x		3√2
cosα=		=		ISEI=		=
	IDSI		2		√2		2

IESI+IFSI=16

8√2x
	=16
2

	16*2		4√2
x=		=		=2√2
	8√2		2

	IFBI		√2		√2
sinα=		=		IFBI=5√2*		=10 IABI=2IFBI=20
	ISBI		2		2

	IDEI		√2		√2
sinα=		=		IDEI=6√2*		=6 ICDI=2IDEI=12
	ISDI		2		2

Z Pitagorasa w trojkacie SBC ICBI=√(6√2)²+(10√2)²=√272=4√17 O=20+12+2*4√17=32+8√17=8(4+√17) Nie jestem pewna czy nie ma błędów rachunkowych bo ciężko się tu liczy

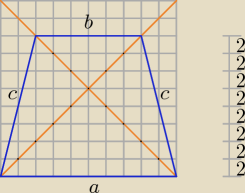
Bogdan: a = 20, b = 12, c = √16² + 2² = √272 = 4√17 L = 20 + 12 + 2*4√17