Dwa rozwiązania - które wybrać? Proszę o podpowiedź :) Zielona Gałązka: Zadanie jest proste ale rozwiązując je różnymi sposobami otrzymałam 2 rozwiązania a tak nie powinno być. Proszę o podpowiedź, dlaczego tak jest.. Treść: rozwiąż nierówność: 3|x − 1| − |1− x| ≥ 8 1. Sposób:wyłączyłam minus przed nawias w drugim nawiasie i mam wyrazy podobne, które mogę zredukować: 3 |x−1| + |x−1|≥ 8 4|x−1|≥ 8 |x−1|≥ 2 rozpatruję dwa przypadki i otrzymuję x−1 ≥ 2 lub −x+1≥ 2 x≥ 3 lub −x ≥1 x ≤ −1 Odp. x należy (−∞, −1) suma (3,∞) 2. Sposób − rozwiązuję tę nierówność jakby te nawiasy nie były wyrazami podobnymi 3|x −1| − |1−x | ≥ 8 Każdy nawias przyrównuję do zera i otrzymuję x=1. Zaznaczam liczbę 1 na osi i rozpatruję dwa przypadki I. (−∞,1) i II. <1, ∞) Ad. I. Ad. II 3(−x+1) − (1−x) ≥ 8 3(x −1) − (−1+x) ≥ 8 −3x +3 −1+ x ≥ 8 3x−3 + 1 − x ≥ 8 −2x ≥ 8 −3+ 1 2x ≥ 8 +3 −1 −2x ≥ 6 2x ≥10 x≤ −3 x ≥ 5 Odp. x należy (−∞, −3) suma (5,∞) Które rozwiązanie jest prawidłowe? :(

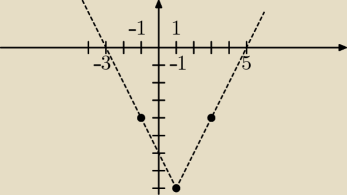
think: no to ja zrobię na swój sposób f(x) = 3|x − 1| − |1− x| − 8 i chcemy aby f(x) ≥ 0 f(−1) = 6 − 2 − 8 = −4 f(1) = −8 f(3) = 6 − 2 − 8 = −4 Odczytuję z wykresu i wychodzi (−∞, −3> ∪<5,∞)

think: a to pierwsze jest źle bo jest taka własność: |−x| = |x| więc żadnego minusa się nie wyłącza przed nawias, bo nie masz z nawiasami do czynienia tylko z wartością bezwzględną, także |1 − x| = |x − 1|

Zielona Gałązka: Think − sprytnie to rozwiązałeś metodą graficzną I Twoja uwaga słuszna. Oczywiście |−x| = |x| Minus, który wyłączyłam niepotrzebnie przed nawias, tak wpłynał na błędne rozwiązanie. Dzięki serdeczne Przyjemnego dnia Ci życzę

think: Zielona Gałązko mam nadzieję zwróciłaś uwagę na to, że oba Twoje rozwiązania miały pewne błędy w drugim zadaniu zabrakło odpowiednich nawiasów a skoro o błędach mowa... to ja nie rozwiązałem, ale rozwiązałam Proszę bardzo i polecam się na przyszłość Bardzo dziękuję, mam nadzieję że miło spędzę dzień czego i Tobie życzę