Logarytmy
Godzio: Dla Kejti
1. Rozwiąż równanie: 2
log√2x =
√2logx2
2. Dana jest funkcja f(x) = log
2(1 − x
2) − log
2(x
2 − x)
a) Wykazać że funkcja jest rosnąca w swojej dziedzinie
| | 1 | |
b) Wykazać, że g(x) = f(x − |
| ) jest nieparzysta (warunek nieparzystości f(−x) = −f(x) ) |
| | 2 | |
3. Rozwiązać nierówność:
log
1253 * log
x5 + log
98 * log
4x > 1
Powodzenia !

Mateusz:
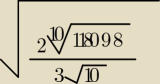
To i ja cos dorzuce mam nadzieje ze nie za łatwe

1) Wykaz ze log
a(x+
√x2−1)+log
a(x−
√x2−1)=0
2)Wykaż że dla dowolnych a,b takich że a>0 b>0 a≠1 b≠1 :
log
a2b
2=log
ab
3) Rozwiąz nierówność |3−log
22x|<1
| | ex+e−x | |
4) Rozwiąż równanie |
| =1
|
| | 2 | |
5) Oblicz(to do rysunku) wskazówka oblicz logarytm tej liczby w liczniku jest pierwiastek 10−go
stopnia z 118098 a w mianowniku jest 3
√10


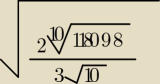 To i ja cos dorzuce mam nadzieje ze nie za łatwe
To i ja cos dorzuce mam nadzieje ze nie za łatwe 1) Wykaz ze loga(x+√x2−1)+loga(x−√x2−1)=0
2)Wykaż że dla dowolnych a,b takich że a>0 b>0 a≠1 b≠1 :
loga2b2=logab
3) Rozwiąz nierówność |3−log22x|<1
1) Wykaz ze loga(x+√x2−1)+loga(x−√x2−1)=0
2)Wykaż że dla dowolnych a,b takich że a>0 b>0 a≠1 b≠1 :
loga2b2=logab
3) Rozwiąz nierówność |3−log22x|<1