nierówności-wytłumaczenie zadania monika: tu jest link do pewnego zadania i komentarzy do niego : https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1805 chodzi mi o to .https://matematykaszkolna.pl/strona/1805.html proszę o wytłumaczenie mi dlaczego w każdym z tych 3 podpunktów inny kierunek znaku jest wstawiany i dlaczego zmieniają się tak znaki . np. 2x+1≤0 , więc |2x+1|= −(2x+1) 6−2x>0 więc |6−2x|= 6−2x dlaczego takie znaki i dlaczego w następnych podpunktach są już inne ? skąd wiedzieć kiedy minus będzie a kiedy plus . Z góry dziękuję

Basia: to wynika z definicji wartości bezwzględnej W dla W≥0 |W| = −W dla W<0 np. W=5 ⇒ |W|=|5|=5=W W= −5 ⇒ |W|=|−5|=5= −(−5)= −W badając |2x+1| rozpatrujesz dwa przypadki 1. 2x+1≥0 ⇔ 2x≥−1 ⇔ x≥ −¹₂ czyli dla x≥ −¹₂ |2x+1|=2x+1 2. 2x+1<0 ⇔ 2x< −1 ⇔ x< −¹₂ czyli dla x< −¹₂ |2x+1|= −(2x+1)=−2x−1 badając |6−2x| postępujesz analogicznie 1. 6−2x≥0 ⇔ −2x≥−6 ⇔ x≤3 czyli dla x≤3 |6−2x|=6−2x 2. 6−2x<0 ⇔ −2x<−6 ⇔ x>3 czyli dla x>3 |6−2x|= −(6−2x)=−6+2x=2x−6

monika: Aha rozumiem w końcu bardzo Ci dziękuję Basiu .

monika: ale Basiu mam jeszcze jedno pytanie . W tym zadaniu rozpatrywane są 3 przypadki bo są trzy przedziały więc dlaczego w każdym z przypadków jest inny znak wstawiany ? od czego to zależy i ską mam wiedzieć kiedy tam będzie plus a kiedy minus .

monika: nie rozumiem dlaczego w pierwszym przypadku mamy 2x+1≥0 a potem w drugim jest 2x+1<0

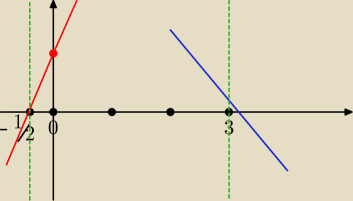
Basia: zajmujemy się obiema wyrażeniami równocześnie, bo występują w jednym równaniu czerwona linia to wykres y=2x+1 niebieska y= 6−2x stąd trzy przedziały: x∊(−∞,−¹₂) ⇒ 2x+1<0 i 6−2x>0 ⇒ |2x+1|=−(2x+1) i |6−2x|=6−2x x∊<−¹₂,3> ⇒ 2x+1≥0 i 6x−2≥0 ⇒ |2x+1|=2x+1 i |6−2x|=6−2x x∊(3,+∞) ⇒ 2x+1>0 i 6−2x<0 ⇒ |2x+1|=2x+1 i |6−2x|= −(6−2x)

monika: aha . czyli zanim zacznie się rozwiązywać najlepiej zrobić sobie oś?

Basia: oś i "falę", albo układ współrzędnych i wykresy można też rachunkowo, ale to więcej pisania; wygląda to wtedy tak 1. 2x+1≥ 0 i 6−2x≥0 ⇔ x≥ −¹₂ i x≤3 ⇔ x∊<−¹₂,3> wtedy |2x+1|=2x+1 i |6−2x|=6−2x i podstawiamy do równania 2. 2x+1≥ 0 i 6−2x<0 ⇔ x≥ −¹₂ i x>3 ⇔ x∊(3,+∞) wtedy |2x+1|=2x+1 i |6−2x|=−(6−2x)=2x−6 i podstawiamy do równania 3. 2x+1< 0 i 6−2x≥0 ⇔ x< −¹₂ i x≤3 ⇔ x∊(−∞,−¹₂) wtedy |2x+1|=−(2x+1)=−2x−1 i |6−2x|=6−2x i podstawiamy do równania 4. 2x+1< 0 i 6−2x<0 ⇔ x< −¹₂ i x>3 to jest niemożliwe; ten przypadek nie zachodzi

monika: a mogę prosić też o oś , falę i ten uklad oraz wykres .

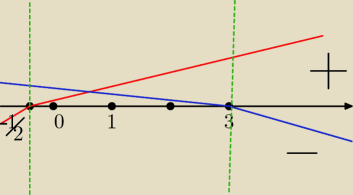
Basia: to ma być fala; plusy nad osią; minusy pod osią czerwone to 2x+1 niebieskie 6−2x

monika: ok

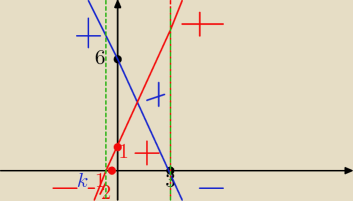
Basia: kolory jak przy fali (to k nie wiem kiedy i po co się wpisało; nic nie znaczy i nie powinno go tam być)

monika: bardzo dziękuję .