Ciąg geometryczny w zadaniach Święty: Witam. Proszę o sprawdzenie zadań. 1) Wyznacz wszystkie wyrazy ciągu a_n= ⁷ⁿ⁻¹¹_2n+3 mniejsze od 1. Sprawdź czy istnieje taka liczba x, że (a₁,x,a₂) jest ciągiem geometrycznym. a₁=−⁴₅ a₂=³₇ a₃=¹⁰₉ Wyrazy mniejsze od jedynki to a₁ oraz a₂ x²=−¹²₃₅ x nie istnieje. 2) Liczby a,b,c są kolejnymi wyrazami ciągu geometrycznego, w którym iloraz jest równy −2. Wartość wielomianu W_(x)= x³+ax²+bx+c dla argumentu 2 jest równa 4. a) Oblicz W₍₋₃₎ b) Oblicz resztę z dzielenia wielomianu W_(x) przez dwumian x+1 a b=−2a c=4a 4=8+4a−4a+4a a=−1 b=2 c=−4 W_(x)= x³−x²+2x−4 a) W₍₋₃₎=−46 b) W₍₋₁₎=−8 Czy zadania są dobrze rozwiązane?

Święty: Podbijam.

Grześ: Sprawdzałem i masz wszystko dobrze, tylko nie jestem pewny dwóch ostatnich punktów a),b), bo tego nie uczyłem się

Święty: Ok, to myślę, a) i b) też są poprawne, bo w a) za x do wielomianu podstawiłem −3, a w b) w grę po prostu wchodzi twierdzenie o reszcie wielomianu. W każdym razie dzieki za pomoc. Pozdrawiam.

Święty: Witam ponownie. Ciekawe zadanie. Dlugosci boków ΔABC tworza ciag geometryczny, a jeden z katow ma miare 60. Oblicz stosunek dlugosci najkrotszego boku do dlugości boku najdluzszego. Coś ruszyłem twierdzeniem cosinusów, ale wychodzą mi dziwne rzeczy. Pokierujcie co i jak.

Święty: Nikt nie wie?

Godzio: Ktoś pewnie wie zaraz zobaczę bo wydaję się fajne zadanko

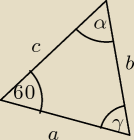
think: możliwe kombinacje kątów 1^o α = γ = 60

	a
wtedy wszystkie boki są równe, ilorazem ciągu geometrycznego jest q = 1 więc		= 1 == q2
	a

2^o α < 60 < γ wtedy najdłuższy bok jest naprzeciwko γ a najkrótszy bok naprzeciwko α i z faktu że tworzą ciąg geometryczny wynika, że najkrótszy to a, b = aq, c = aq²

c		aq2
	=		= q2
a		a

3⁰ γ < 60 < α robi się analogicznie tylko boki się zmieniają. Także stosunek najdłuższego do najkrótszego wynosi q². Można się pokusić o stwierdzenie, że tak czy siak bok b, będzie tym którego długość będzie środkowa, czyli b² = a² + c² − 2accos60

	b
i bez znaczenia czy a =		a c = bq czy na odwrót...
	q

	b2		1
b2 =		+ b2q2 − 2b2*		/*q2
	q2		2

b²q² = b² + b²q⁴ − b²q² b²q⁴ − 2b²q² + b² = 0 b²(q⁴ − 2q² + 1) = 0 b²(q² − 1)² = 0 ⇔ q² − 1 = 0 ⇔ q = 1 odpada przypadek q = −1 bo długości boków nie mogą być ujemne.

Godzio: think tak się zastanawiam czy jeśli rozpatrujemy te 3 przypadki gdzie może być kąt to długości boków nadal zostają w tym samym stosunku ? tzn że zawsze a jest najmniejsze b jest średnie, a c największe ?

think: zawsze b jest średnie natomiast zmienia się a i c, ale zauważ że policzenie tego drugiego przypadku jest w pełni symetryczne. Zresztą i tak wychodzi, że ten trójkąt jest równoboczny

Godzio: dla wszystkich przypadków jest równoboczny ? bo mi tak wychodziło i stwierdziłem że chyba coś źle rozumuje

think: no dobra pewnie miałam wstawić tak ≤ zamiast ostrych ale masz jakiś krótszy sposób rozumowania, bo zauważyłam, że ostatnio często jeżdżę z opola do wrocławia przez poznań

Godzio: nie, nie

Święty: Dzieki za pomoc.

Święty: Cześć. Mam dla Was kolejne, mam nadzieję kontrowersyjne zadanie. Dany jest ciąg a₁=8, a₂=88, a₃=888, a₄=8888, ... Oblicz sumę 50 początkowych wyrazów tego ciągu. Wyszło mi S₅₀=^{8(1051−460)}₈₁ Czy wynik jest dobry?

Święty: Podbijam