proszę.. Edka: Ile wynosi CD, AE, BF?

sushi_gg6397228: podobienstwo trojkatow CDA i BFA

Edka: CD = BF?

sushi_gg6397228: |CD| to nawet z Pitagorasa mozna policzyc trojkat rownoramienny ACB wiec |BF|= |EA|

Edka: CD = 15?

sushi_gg6397228: napisalem podobienstwo, a nie przystawanie jak narysujesz sobie te dwa trojkaty, to zobaczysz ze przecwiprostokatne maja 17 i 16, wiec CD≠BF

Edka: nic z tego niewem:(

sushi_gg6397228: podalem wierzcholki w jakiej kolejnosci sa boku podobne, policz CD z Pitagorasa, a potem uloz odpowiednie boki na proporcje

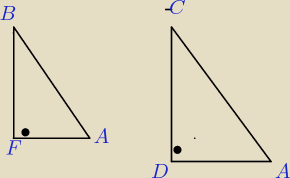
sushi_gg6397228: zauwazylem, ze policzylas juz CD=15 to teraz rysujemy dwa trokaty prostokatne CDA i BFA kat prosty w wierzcholku D i F

Edka: BF = 14?

sushi_gg6397228:

sushi_gg6397228: zapisz tutaj obliczenia, a nie rzucasz liczbami

Edka: Naprawdę nie wiem, możesz wytłumaczyć całość? |CD| z twierdzenia Pitagorasa, reszty nie ruszę..

sushi_gg6397228: narysowalem dwa trojkaty, uloz proporcje z podobienstwa, podpisz boki liczbami, ktore masz dane

Edka: ^AD_AC=^AF_AB

sushi_gg6397228: troche Ciebie oszukalem z tym podobienstwem, bedzie tak trojkat CDA i tw cosinusow 15²= 8²+17² −2*8*17 * cos (kata A) z tego wyliczymy cos (kata A)=.. potem trojkat AFB

	|BF|
cos (kata A)=		===> |BF|=...
	|AB|

Edka: dobra to już nie ma sensu.. dzięki za pomoc, pozdrawiam

sushi_gg6397228: ma sens, bo źle zobaczylem na te katy, to ostatnie jest dobrze

sushi_gg6397228: jednak to bylo dobrze, wiec masz do tamtego inna proporcje

AC		AB
	=
CD		BF

17		16
	=		==> BF= ...
15		BF

porownaj wyniki, powinno wyjsc to samo

Siostra Ewa: Ale flejtuchy!Rozgrzebaliście zadanie,nie kończycie i jeszcze podajecie błedne odpowiedzi.Zupełnie jak ci azjatyccy ignoranci,którzy budowali most na rzece Kwai,a on ciągle się zawalał. A tymczasembliczmy AE Rozpatrzmy w tym celu trójkąt BAE i oznaczmy∡BAE=α₁,∡ABE=β Z twierdzenia sinusów mamy:

AE		AB		AB
	=		=
sinβ		sin[180−(α1+β)]		sin(α1+β)

cosβ=⁸₁₇ , sinα₁=²⁴⁰₂₈₉[jak to policzyć?] Teraz macie wystarczająco danych,aby policzyć AE.Miłej zabawy!