W trójkącie ABC P: W trójkącie ABC mamy dane |AC|=|BC|=13 cm, |AB|=10cm. Z punktu E należącego do wysokości CD poprowadzono odcinek EF długości 3 cm, prostopadły do ramienia AC, F należy do odcinka AC. Oblicz pole trójkąta CFE oraz długość odcinka ED.

archeolog:

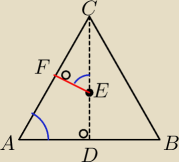
vaultboy: AD=5cm bo wysokość w trójkącie równoramiennym dzieli bok na połowę ΔCEF≈ΔCAD (kkk) Możemy wyliczyć tę skalę podobieństwa FE/AD=3/5 k=3/5 CF/CD=3/5 wyliczmy CD z Pitagorasa CD=12 zatem CF=36/5 Pole CFE wynosi (CF*FE)/2=(36/5 * 3)/ 2=54/3 3/5=CF/CD=CF/(CE+ED) dalej sam dasz radę

Eta: zadanie sprzed 5 lat

Eta: P... pewnie już w Anglii na" zmywaku"