odwrotnosc funkcji Cinu: Znajdz wzor fukncji odwrotnej do kazdej z podanych funkcji: y = 3x odwrotnosc

1
	x
3

x−5 odwrotnosc to x + 5 nie rozumiem {1}{2} x + 3 odwrotnosc to 2x + 6 Help

Krzysiek: weźmy y = 3x ta funkcja przyporządkowuje argumentom: 1 , 2 , 3 , 100 wartości: 3 , 6 , 9 , 300 Funkcja odwrotna to taka, która przypisze argumentom: 3 , 6 , 9 , 300 wartości: 1 , 2 , 3 , 100

	1
Argumenty zawsze nazywamy x , a wartości y więc odpowiedź to: y =		x
	3

Ale wystarczyło zrobić to tak:

	1
y = 3x ⇒ x =		y
	3

I stąd podać odpowiedź. Pomyśl dlaczego.

Cinu:

	6
ile będzie
	x

Krzysiek: nie wiem o co pytasz

Cinu: odwrotnosc

Krzysiek:

	6
Też		, ale już więcej za ciebie nie zrobie.
	x

Cinu: spoko . Różnowartosciowość jeszcze mnie została Czy podana funkcja jest roznowartosciowa? a)y = 2 |x| b)y = (x−2)² a) 2x₂ − 2x₁ = 2(x₂− x₁) << jest różnowartościowa b) (x²₂ −2x₂ + 4) − (x²₁ −2x₁ + 4) = x²₂ − x²₁ << Ta funkcja nie jest różnowartościowa z powodu ². Czy jest dobrze?

Krzysiek: a) źle b) dobry wniosek, ale chyba ze złego rozumowania Wytłumacz jak to sprawdzasz.

Cinu: f. roznowartosciowa − argument przyjmuje inna wartość np. z zad. b) −1 ² = 1 1² = 1 nie jest a ) 2* |−1| = 2 2* |1| = 2 nie jest

Krzysiek: Ano właśnie Ja to bym wziął i je po prostu narysował. PS. To było (a)

Cinu: teraz to juz wogole tego nie rozumiem . Chcialem sie uczyc rozszezonej matmy z kl 1 (jestem w 3 Technikum) ale chyba nic z tego.

Cinu: mogłbys pomóc?

Krzysiek: Różnowartościowa funkcja to taka, która ma tą samą wartość dla paru argumentów. np. sin(x) ma tą samą wartość 0 dla x = 0, 180, 360 [stopni] , itd.

Krzysiek: qrde, tzn to co napisałem to jest taka która NIE JEST różnowartościowa

Cinu: no właśnie, jakbyś udowodnił przykład a oraz b?

Krzysiek: Nie zastanawiaj się o co mi chodziło z tym "PS to było (a)". Ja też nie wiem

Krzysiek: Tak jak ty już to zrobiłeś

Krzysiek: w (a) mamy tą samą wartość 1 , dla argumentów −1 i 1

Cinu: 2x + 6 = 2(x₂ − x₁ ) << jest x² + 4x + 1 = x₂² − x₁² << nie jest

1
	x − 3 = {1}{2} ( x2 − x1) << jest
2

2x³ = 2( x₂ − x₁ ) ³ << jest, dlaczego? przeciez −1 ³ = −1, 1³ =1

1
	= 1 : (x1 − x2) << jest, dlaczego?
x

jak to się udowodnic?

Krzysiek: To jest proszę pana jakaś taka formalna procedura na udowadnianie tego. Ja zawsze rysuję funkcję, ale jeśli koniecznie chcesz, to to jest jakoś tak: Chodzi o to, że obliczamy wartości funkcji w x₁ i x₂ i odejmujemy je od siebie. Jeśli może wyjść zero, to znaczy że wartość w x₁ i w x₂ jest taka sama, czy funkcja nie jest różnowartościowa. Ale uważaj! x₁ nie może się równać x₂, bo jakby się równały no to wiadomo że wyjdzie zero. Np. f(x) = x² x₁² − x₂² = 0 ⇒ ( x₁ − x₂ )( x₁ + x₂ ) = 0 Może być zero dla x₁ = −x₂

Cinu:

	1
jak to rysujesz? np
	2

Tabelka x₁ 1 2 3

	1		1
1
	2		3

x₂ 4 5 6

1		1		1
4		5		6

Krzysiek:

	1
teraz mówisz o f(x) =		?
	x

Pytanie jeszcze takie pomocnicze: w której jesteś klasie?

Cinu: Tak. 3 technikum informatyczne za poltora roku matura z matmy podstawowej mam dobre oceny (4 oraz 5) wiec sprobowalem troche trudniejsze.

Cinu: dobra chyba zrozumialem za f(−1) = −1 dla f(1) = 1

	1
dla f(2) =
	2

	1
dla f(−2) = −
	2

Cinu: dobrze rozumiem?

Krzysiek:

	1
Rysuję f(x) =
	x

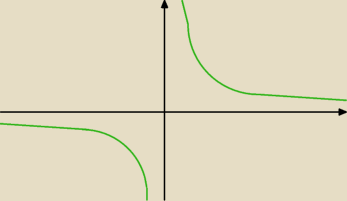
I widać że żadne wartości się nie powtarzają

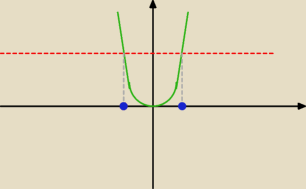
Krzysiek: Rysuję f(x) = x² I widać że się powtarzają: np w dwóch iksach zaznaczonych na niebiesko jest ta sama wartość

Cinu: dobra, dziękuję za poświęcony czas, "natchnienie zaszło i zrozumiałem" teraz odwrotnośc funkcji , przekształcanie oraz składanie dzisiaj zrobię i będzie git. W technikum jedyne przedmioty warte nauki to matematyka, fizyka i zawodowe (systemy operacyjne, urzadzenia tech.komp, oprogramowanie biurowe(to nie jest przedmiot oraz programowanie strukturalne i obiektowe (easy))

Krzysiek: No to poczytaj. A przy odwrotności funkcji pamiętaj znów obrazkowy pogląd na sprawę: Wykres funkcji odwrotnej do f(x), to odbicie wykresu funkcji f(x), względem prostej y = x

Cinu: zaczynam pojmować. PS Ktora ty klasa?

Krzysiek: fizyka, II rok

Cinu: studia z fizyki?(jak tak) trudno jest? Ja chcę zdawać mature z mat. rozszerzonej(jak sie uda) oraz fizyke podstawowa i na AiR lub Informatyke pojsc.

Krzysiek: No bardzo fajne kierunki, zwłaszcza ten pierwszy. Ja wiem czy trudno − nie myślę w ten sposób. Kocham ten przedmiot i nigdy w życiu nie mógłbym studiowac niczego innego

Cinu: dasz gg

mac: A w jakim to mieście można spytać ?

Krzysiek: Ty daj.

Cinu: 7474077

mac: @Krzysiek: w jakim mieście studiujesz?

Krzysiek: w Oxfordzie

mac: haha, good joke

Krzysiek: a jednak

mac: ja tam planuje iść do Wrocławia na informatykę − może się ktoś orientuję jak tam jest? Ale to dopiero w 2012

meduza1707: y=2x−4