Promien podstawy stozka.. Marek: Powierzchnia boczna stozka po rozwinieciu jest polkolem o promieniu 12 cm. Podstawa stozka jest kolem o promieniu

Kejti: oblicz obwód powierzchni bocznej. potem przyrównaj to do wzoru na obwód wycinka..

Marek: ale nie mam podanych danych zeby obliczyc Pb stozka. Podana jest tylko ze po rozwinieciu Pb jest polkolem o promieniu 12 cm ...

Kejti: masz półkole znaczy wycinek koła o kącie 180^o wzór:

α
	*2πr=...
360o

Marek: niestety ale nie rozumiem ... mozesz mi to jakos przytoczyc w latwiejszy sposob ?

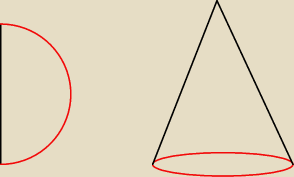
Kejti: to po lewej to powierzchnia boczna po rozwinięciu, po prawej stronie masz narysowane jak to wygląda gdy ta powierzchnia jest na stożku. Kolorem czerwonym jest zaznaczone jak się ma obwód powierzchni bocznej po rozwinięciu do obwodu podstawy. tzn. są sobie równe, teraz rozumiesz?

Marek: Aha czyli wynika z tego ze podstawa stozka tez bedzie miala 12 .

Marek: A takie zadanie .

	x+3
Liczba rozwiazan		= 0 jest rowna
	(5−x)(x+2)

A−3 B−2 C−1 D−0 Chodzi tutaj aby mianownik przyrownac do 0 ?

Kejti: nie, nie będzie miała promienia równego 12, musisz obliczyć obwód powierzchni bocznej z tego wzoru który podałam, a potem przyrównać to do zwykłego wzoru na obwód i wylicz promień.

Marek: podstawic mam za α=180 za r=12 za π=3.14 tak

Kejti: π nie musisz przybliżać.. to się później skróci

Tepy: czyli wyjdzie 12π tak

Tepy: teraz mam podstawic do zyklego wzoru na obwod V=¹₃πr²h

Tepy: ale nie mam podanej wysokosci to jak mam to wyliczyc

Kejti: oj Marku, Marku.. to nie jest wzór na obwód tylko objętość..

Marek: aha nie znajomosc wzorow a jaki jest wzor na obwod

Marek: P=πr(r+l)

Kejti: Ob=2πr

Marek: ale to po co liczylem wczesniej tam te rzeczy gdzie mam podstawic tamte wyliczenia teraz

Kejti: zapisz to sobie..: pole koła: P=πr² pole wycinka:

	α
Pw=		*πr2
	360o

obwód koła: Ob=2πr lub Ob=πd gdzie d to średnica obwód wycinka:

	α
Obw=		*2πr
	360o

Objętość stożka:

	1
V=		*πr2*H
	3

pole powierzchni bocznej: P_b=πrl gdzie l to długość tworzącej pole powierzchni całkowitej: P=πr(r+l)

Kejti: Ob_w=12π Ob_p=Ob_w 12π=2πr Ob_p to obwód podstawy..

Marek: OB=12 tak

Kejti: obwód powierzchni bocznej i obwód podstawy to 12π.

Marek: To w takim razie podstawa stozka jest kolem o promieniu 6

Kejti: tak

Tepy: no nareszcie niby latwe a zamotane jak ... A to zadanko z ktorym sie pospieszylem nieco i jest troche wyzej

Kejti: mianownik przyrównujesz do zera wtedy kiedy masz do policzenia dziedzinę. tutaj:

x+3
	=0
(5−x)(x+2)

ułamek równy jest zero wtedy gdy licznik równy jest zero.. x+3=0

Marek: ale jak przyrownam mianownik do 0 to x=−3 a takiej odp nie ma

Kejti: masz obliczyć ilość rozwiązań.. a nie podać rozwiązanie ;>

Marek: odp bedzie ze sa 3 rozwiazania

Kejti: ech.. facet. masz x=−3 znaczy, że rozwiązaniem tego równania jest liczba −3. to jaka jest liczba rozwiązań?

Marek: 0

Kejti: poddaję się..

Kejti: to równanie nie ma rozwiązania?

Marek: aha czyli ze 1

Marek: ja juz sam nie wiem Matematyka to jest czarna magia jakas