nierówność Paulina: Rozwiąż nierówność x² − x − 2 ≤ 0

mac: jaki problem?

Paulina: z narysowaniem póżniej na lini wyniku ... wychodzi mi −1 i 2

mac: Δ = 1 + 4 = 5 √Δ = √5

	1 − √5
x1 =
	2

	1 + √5
x2 =
	2

mac: Ups sory, powinno być delta 3

Paulina: no własnie wynik mam dobry tylko jak to potem przedstawić na tej lini

mac: czyli; √Δ = 3

	1 − 3
x1 =		= −1
	2

	1 + 3
x2 =		= 2
	2

Paulina: to się zgadza a co dalej?

mac: Zaraz sobie narysuje i podam wynik

Paulina: super dzięki

mac: x∊<−1;2>

Paulina: dzięki

Paulina: Kąt α jest ostry i tg α wynosi 512. Oblicz cos α. Jeszcze to jeśli można

Paulina: tg wynosi ⁵₁₂

mac: https://matematykaszkolna.pl/strona/1541.html tu masz podobne zadanie

mac: w tym roku maturka?

Paulina: no niestety

mac: hehe, jak podstawowa to dasz radę , prosta jest

Paulina: no ma być troszkę trudniejsze ...

Paulina: wyszło mi super

mac: taak? gdzie tak pisze, nigdzie o tym nie czytałem chociaż maturkę mam za rok, ale zbyt trudniejszej matury nie mogą zrobić jak chcą aby były zadowalające wyniki xD

mac: gratki

Paulina: tak nam mówi babka z maty ... zobaczymy jak to będzie

mac: Zobaczymy, może ona chciałaby aby dać troche trudniejsze zadania, np otwarte. bo zamkniętych raczej zmienić nie mogą . − bo odebraliby nadzieję tym słabszym. Gdyby takie zadania były na maturce z polaka

Paulina: ja tam wolę polski

Paulaaa: 2x² + x+ 1≤0 pomóżcie mi rozwiązać nierowność

Gustlik: x²−x−2 ≤ 0 Δ=1−4*1*(−2)=9 √Δ=3

	1−3
x1=		=−1
	2

	1+3
x2=		=2
	2

x∊<−1, 2>

Piotr: a do czego to Gustlik ?

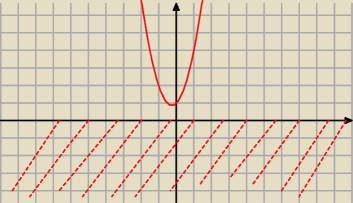
Gustlik: 2x²+x+1≤0 Δ=1²−4*2*1=−7 brak pierwiastków Obszar rozwiązań nierówności (≤0) obejmuje punkty na osi OX i pod nią (zaznaczyłem czerwonymi przerywanymi liniami). Parabola natomiast "wisi" nad osią OX i wobec braku miejsc zerowych nie ma punktów wspólnych ani z osią OX ani z obszarem rozwiazań nierówności, zatem x∊∅.