
| 2x+3 | ||
Proszę o sprawdzenie.. znajdź dziedzinę funkcji: f(x) = | ||
| 2 |
| 2x+3 | ||
−1 ≤ | ≤ 1 | |
| 2 |
| 2x+3 | |
≥ −1 | |
| 2 |
| 2x+3 | |
+ 1 ≥ 0 | |
| 2 |
| 2x+5 | |
≥ 0 | |
| 2 |
| 5 | ||
x ≥ − | ||
| 2 |
| 2x+3 | |
≤ 1 | |
| 2 |
| 2x+3 | |
− 1 ≤ 0 | |
| 2 |
| 2x+1 | |
≤ 0 | |
| 2 |
| 1 | ||
x ≤ − | ||
| 2 |
| 5 | 1 | |||
Odp: x ∊ <− | , − | > | ||
| 2 | 2 |
| 2x + 3 | ||
f(x) = | ||
| 2 |

| 2x+3 | ||
f(x)= | ||
| 2 |

| 2x+3 | ||
f(x) = arc sin | ||
| 2 |


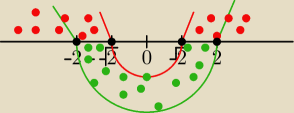 jeszcze jedno: f(x) = arc cos (x2 − 3)
−1≤ (x2 − 3) ≤ 1
x2 − 3 ≥ −1
x2 − 2 ≥ 0
(x − √2 )(x + √2) ≥ 0
x = √2 i x = −√2
x ∊ (−∞, −√2> i <√2, +∞)
x2 − 3 ≤ 1
x2 − 4 ≤ 0
(x−2)(x+2) ≤ 0
x=2 i x=−2
x∊ <−2, 2>
odp: x ∊ <−2, −√2 > i <√2, 2>
jeszcze jedno: f(x) = arc cos (x2 − 3)
−1≤ (x2 − 3) ≤ 1
x2 − 3 ≥ −1
x2 − 2 ≥ 0
(x − √2 )(x + √2) ≥ 0
x = √2 i x = −√2
x ∊ (−∞, −√2> i <√2, +∞)
x2 − 3 ≤ 1
x2 − 4 ≤ 0
(x−2)(x+2) ≤ 0
x=2 i x=−2
x∊ <−2, 2>
odp: x ∊ <−2, −√2 > i <√2, 2>  jakieś dziwne mi się wydaje..
jakieś dziwne mi się wydaje..

 mam jeszcze 4 takie, ale nie mam siły już na nie dziś.. pewnie jutro się z nimi zmierzę.
dzięki wielkie
mam jeszcze 4 takie, ale nie mam siły już na nie dziś.. pewnie jutro się z nimi zmierzę.
dzięki wielkie
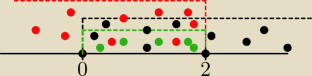 więc mam kolejny przykład do sprawdzenia..
f(x) = √arc sin (x−1)
1) src sin (x−1) ≥ 0
z wykresu −> x ∊ <0,2>
2) −1 ≤ x−1 ≤ 1
x−1 ≥ −1
x ≥ 0
x−1 ≤ 1
x ≤ 2
odp: x ∊ <0,2>
więc mam kolejny przykład do sprawdzenia..
f(x) = √arc sin (x−1)
1) src sin (x−1) ≥ 0
z wykresu −> x ∊ <0,2>
2) −1 ≤ x−1 ≤ 1
x−1 ≥ −1
x ≥ 0
x−1 ≤ 1
x ≤ 2
odp: x ∊ <0,2>
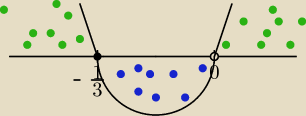 jeszcze jeden:
jeszcze jeden:
| 2x+1 | ||
f(x) = arc sin | ||
| x |
| 1 | ||
x= − | i x=0 | |
| 3 |
| 1 | ||
x= − | i x=0 | |
| 3 |
| x+1 | ||
i ostatni.. f(x) = arc tg | ||
| 2x2 |
