Rozwiąż nierówność z wartością bezwzględną. abc: a) |x²+5x+2|≥1 (wychodzi mi przedział (−∞;−4.56>∪<−0.43;+∞) − nie wiem czy dobrze. b) |x+3|−|x|>1 Prosiłbym o pomoc, rozwiązanie.

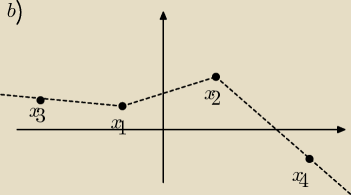
think: ad a)Policz deltę i pierwiastki dla x ∊ (−∞, x₁> ∪<x₂,∞) rozwiązujesz taką nierówność: x² + 5x + 2 ≥ 1 dla x∊<x₁,x₂> rozwiązujesz: −x² − 5x − 2 ≥ 1 b) polecam rozwiązać graficznie f(x) > 0 f(x) = | x + 3| − |x| − 1 narysowanie takiego wykresu jest dość proste, wybierasz punkty dla których zerują się wartości w module oraz jakieś dwa punkty które leżą na lewo i prawo od tych punktów, czyli np x₁ = −3 x₂ = 0 to na lewo od mniejszego x₁ będzie np x₃ = −5 a na prawo od większego może być x₄ = 1 rysunek obrazuje jak łączyć te punkty ale nic więcej, powodzenia, jak zrobisz tutaj to powiem Ci czy dobrze. No i z wykresu już łatwo odczytać, dla jakich x−ów funkcja przyjmuje wartości dodatnie.

Slawek: Zrobiłem to inaczej. Nie jestem pewien czy dobrze. |x+3|−|x|>1 Miejsca zerowe to −3 i 0 więc mam przedziały: (−∞;−3> (−3;0> (0:+∞) 1. dla x ∊ (−∞;−3> x+3 ≤0 więc |x+3|=−(x+3)=−x−3 x<0 więc |x|=−x −x−3+x>1 −3>1 Sprzeczność 2. dla x ∊ (−3;0> x+3>0 więc |x+3|=x+3 x≤0 więc |x|=−x x+3+x>1 2x>−2 x>−1 x ∊ (−1;+∞) Część wspólna (−3;0> i (−1;+∞) to (−1;0> 3. dla ∊ (0:+∞) x+3>0 więc |x+3|=x+3 x≥0 więc |x|=x x+3−x>1 3>1 Zgadza się. Rozwiązaniem tej nierówności jest przedział (−1;+∞) Dobrze to rozwiązałem?

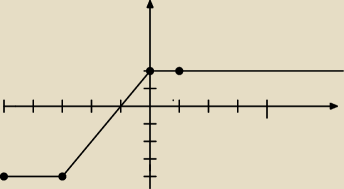
think: sprawdźmy moim sposobem f(−5) = 2 − 5 − 1 = −4 f(−3) = −3 − 1 = −4 f(0) = 2 f(1) = 2 ma być > 0 zatem rozwiązanie to (−1,∞)

Slawek: Dzięki wielkie za pomoc!