Ogrodnik ma 139 metrów bieżących siatki ogrodzeniowe kloops: Ogrodnik ma 139 metrów bieżących siatki ogrodzeniowej. Chce ogrodzić prostokątną działkę i podzielić ją siarką na cztery mniejsze prostokątne działki równej szerokości, których długość jest równa szerokości całej działki. Jeżeli długość całej działki ma co najwyżej 42 m, to jaka może być jej szerokość?

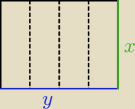
Dorota: Cześć, Cała siatka musi wystarczyć na 5 ∧ szerokość i 2∧długośc. Czyli 139 = 5x + 2y ⇔ 2y = 139 − 5x Wiemy że y ≥ 42 Zatem 139 − 5x = 2y ≥2 * 42 czyli 139 − 5x ≥ 84 po rozwiązaniu nierówności otrzymujemy x ≤ 11.

Dorota: Oczywiście dodatkowo x>0.

Dorota: Jeszcze jedna uwaga. W zadaniu jest napisane, że w tych małych działkach długość jest równa szerokości tej całej dużej działki. Jeżeli uznamy dodatkowo, że długość musi być dłuższa niż szerokość, to należy jeszcze dodać ograniczenie: x > y/5 ⇔ 5x > y ⇔ 5x > 42 czyli dodatkowo x > 8,4. Podsumowując: jeżeli zakładamy, że długość musi być dłuższa niż szerokość, to x ∊ (8,4;11>

kloops: proszę o poprawne rozwiązanie.

kloops: Chciałbym odnowić temat, myślę, że jest tu ktoś, kto potrafi to zrobić?

Grześ: kloops, tam jest jeden błąd, bo jest napisane że długość może być co najwyżej 42m czyli y≤42

Grześ: a nie y≥42

Grześ: Znaczy się nie tak, już rozpisze Ci rozwiązanie:

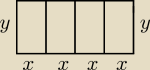
Grześ: Ten sam rysunek co na górze: Czyli suma długości ogrodzenia wynosi: 2y+5x=139 ⇒ 2y=139−5x oraz długość całej działki mniejsza lub równa 42m: y≤42 139−5x≤84 −5x≤−55 x≥11 Poza tym mamy warunek na to, żeby długość nie byłą mniejsza od szerokości:

	y
x>
	4

4x>y 4x>42 x>10,5 Czyli spełnionej obu tych warunków jest: x∊<11,+∞)

kloops: właśnie coś mi tu nie pasuje. bo jak sam robiłem to zadanie, to też mi wychodziło tak jak tobie Grzesiek. A w odpowiedzi podają, że ma być przedział <11 , 27,8) więc od góry granica musi być jakaś inna. Poza tym, dlaczego założyłeś, że długość ma być mniejsza od szerokości, skoro w zadaniu pisze, że ma być jej ona równa? Chyba, że w odpowiedziach jest błąd? Eta, Bogdan, pomocy

kloops: Chodzi mi o to, że do tego zdania: "...których długość jest równa szerokości całej działki" wydaje mi się, że powinno być takie równanie: y/4=x y=4x 4x<42 x<10,5 ale wtedy wyszedłby zbiór pusty, więc coś jest nie tak.

Avc: 4x ≤ 42 x≤10.5 x∊(0 ; 10.5) 5y+8x=139 y=^139−8x₅=f(x) y_min=11 dla x=10.5 y_max to granica funkcji f(x) dla x→0 lim ^139−8x₅ = ¹³⁹⁻⁰₅ = 27.8 x→0 Więc y ∊ <11 ; 27.8) Prawostronnie otwarty, bo 27.8 to wartosć dla x=0, a x>0

Avc: "...których długość jest równa szerokości całej działki" y jest szerokością całej działki a zarazem długością tych małych. y>x Ja bym to tak interpretował

Avc: Tam na początku ma być: x∊(0 ; 10.5> *

Bogdan: Dzień dobry. Przepraszam, że nie włączyłem się do rozmowy, ale nie śledziłem tego wątku i nie zauważyłem skierowanej do mnie i do Ety prośby o pomoc. Przechodzę do zadania. Obliczanie granicy jest tu zbędne, zresztą obliczanie granic nie jest w programie nauczania w szkole średniej. − szerokość działki: x ≥ 0. − długość działki: 0 ≤ y≤ 42.

	5		139
5x + 2y = 139 ⇒ y = −		x +
	2		2

	5		139		2
0 ≤ −		x +		≤ 42 / * −
	2		2		5

	139		84		139		139		84
0 ≥ x −		≥ −		⇒		≥ x ≥		−
	5		5		5		5		5

	55		139
		≤ x ≤		⇒ 11 ≤ x ≤ 27,8
	5		5

Np.: x = 11 i y = 42, x = 13 i 37, x = 15 i y = 32, itd., oczywiście długości te nie muszą wyrażać się liczbami całkowitymi.

kloops: Wsystko pięknie, ładnie, dzięki wam obojgu za pomoc, tylko Bogdan, tam chyba przy twoim założeniu powinno na początku y>0, bo długość nie może być równa 0.

Bogdan: Tak, y > 0. Gratuluję spostrzegawczości.