Funkcje na koło konio: Witam Chciałbym poprosić o rozwiązanie kilku zadań z funkcji które mam przedstawić w postaci wykresu. |x−3|−|x+2| |x|−|x² −1| 2|x² −|x||+2

	x2 −9
ln
	|x|+3

cosx
|cosx|

	1
arcsin
	3

	π
tg(x+		)
	6

e⁻2 sinx e^x cosx log¹₂ |x−1| e⁽−x−2) sh|x+1| − mógłby mi ktoś wytłumaczyć co to za funkcja sh Proszę o wytłumaczenie przykładów ponieważ mój profesor z matematyki urządza kolokwium z funkcji to są przykładowe funkcje. Pomocy bo obleje

Godzio: pomogę w 1,2,3,5,10 przykładzie

	π		π
z tg(x +		) −− wystarczy przesunąć wykres tgx o		w lewo
	6		6

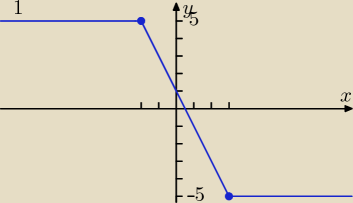Godzio: f(x) = |x − 3| − |x + 2| −− wykres rysuje się w przedziałach więc trzeba rozpatrzeć przypadki 1^o x ∊ (−∞,−2) f(x) = −x + 3 − (− x − 2) = −x + 3 + x + 2 = 5 2^o x ∊ <−2,3) f(x) = −x + 3 − (x + 2) = −x + 3 − x − 2 = −2x + 1 3^o x ∊ <3,∞) f(x) = x − 3 − (x + 2) = x − 3 − x − 2 = −5 I tak samo w drugim przykładzie: f(x) = |x| − |x² − 1| x² − 1 ≥ 0 ⇒ x ∊ (−∞,−1) ∪(1,∞) 1^o x ∊ (−∞,−1> f(x) = −x − (x² − 1) = −x − x² + 1 = −x² − x + 1 2^o x ∊ (−1,0) f(x) = −x − (−x² + 1) = x² − x − 1 3^o x ∊ <0,1) f(x) = x − (−x² + 1) = x² + x − 1 4^o x ∊ <1,∞) f(x) = x − (x² − 1) = −x² + x + 1 Ten drugi wykres to już sam sobie narysujesz bo chyba umiesz rysować parabolę Zaraz dalsza część

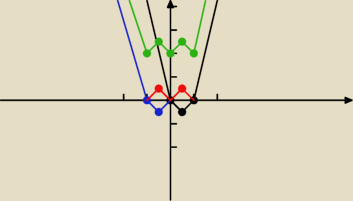Godzio: 3. f(x) = 2|x² − |x|| + 2 Mamy tu 3 przekształcenia funkcji 2x² − 2x

	1		1
Krok pierwszy: rysujemy funkcję f(x) = 2x2 − 2x = 2x(x − 1) = 2(x −		)2 −
	2		2

	1		1
x1 = 0, x2 = 1, p =		, q = −
	2		2

Krok drugi: symetria częściowa względem OY ( f(|x|) ) otrzymamy wykres: f(x) = 2x² − 2|x| Innymi słowy wymazuje to co jest po lewej i odbijam to co jest po prawej Krok trzeci: symetria częściowa względem OX ( |f(x)| ) otrzymamy wykres: [C[f(x) = |2x² − 2|x|| To co jest poniżej osi OX odbijamy na górę Krok czwarty: cały wykres podnoszę o 2 jednostki do góry i otrzymujesz końcowy wykres

Godzio:

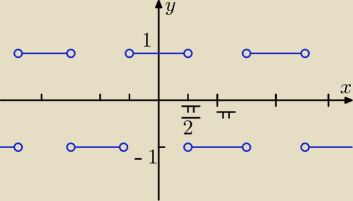
	cosx		π
f(x) =		x ≠		+ kπ
	|cosx|		2

	cosx
1o cosx < 0 ⇒ f(x) =		= − 1
	−cosx

	cosx
2o cosx ≥ 0 ⇒ f(x) =		= 1
	cosx

Jack:

	ex−e−x
sh (x) − to sinus hiperboliczny. sh x =
	2

Godzio:

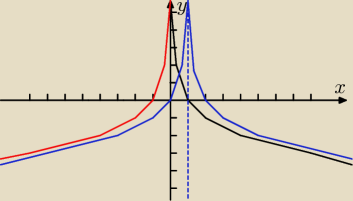
	1
Obstawiam że podstawa jest		: f(x) = log1/2|x−1|
	2

I znów mamy 2 przekształcenia, rysujesz wykres: f(x) = log_1/2x następnie mamy przekształcenie f(|x|) i na końcu cały wykres przesuwasz o 1 jednostkę w prawo