 Podstawa graniastosłupa prostego jest trójkat równoramienny o kącie miedzy ramionami
120 stopni i podstawie długosci 12. Długosc wysokości graniastosłupa jest równa długosci
promienia okregu opisanego na podstawie graniastosłupa ,Wyznacz objetośc graniastosłupa
Podstawa graniastosłupa prostego jest trójkat równoramienny o kącie miedzy ramionami
120 stopni i podstawie długosci 12. Długosc wysokości graniastosłupa jest równa długosci
promienia okregu opisanego na podstawie graniastosłupa ,Wyznacz objetośc graniastosłupa
 Nigdy nie byłem dobry z okręgów opisanych i wpisanych, ale to powinno być coś takiego:
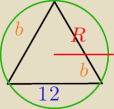
R=a/2sinα −a dowolny bok, α − kąt naprzeciw tego boku
R=12/2sin120=12*2/√3=24/√3=8√3
Obj: V=Pp*H ,Pp−pole podstawy, H−wysokość
Potrzebna jest nam jeszcze długość reszty boków trójkąta.
Możemy ją obliczyć ze wzoru:
2R=b/sinβ
Wiemy, że jest to trójkąt równoramienny, czyli kąty między ramionami muszą wynosić:
180−120/2=30[stopni]
16√3=b/sin30(stopni)
16√3=b/0,5 |*2
32√3=b
Pp=0,5(32√3+32√3+12)=32√3+6
V={32√3+6)*8√3=256*3+42√3=768+42√3
Odp: Objętość tego graniastosłupa wynosi 768+42√3 [cm]
Nie jestem pewien, więc nie daje gwarancji
Nigdy nie byłem dobry z okręgów opisanych i wpisanych, ale to powinno być coś takiego:
R=a/2sinα −a dowolny bok, α − kąt naprzeciw tego boku
R=12/2sin120=12*2/√3=24/√3=8√3
Obj: V=Pp*H ,Pp−pole podstawy, H−wysokość
Potrzebna jest nam jeszcze długość reszty boków trójkąta.
Możemy ją obliczyć ze wzoru:
2R=b/sinβ
Wiemy, że jest to trójkąt równoramienny, czyli kąty między ramionami muszą wynosić:
180−120/2=30[stopni]
16√3=b/sin30(stopni)
16√3=b/0,5 |*2
32√3=b
Pp=0,5(32√3+32√3+12)=32√3+6
V={32√3+6)*8√3=256*3+42√3=768+42√3
Odp: Objętość tego graniastosłupa wynosi 768+42√3 [cm]
Nie jestem pewien, więc nie daje gwarancji 
| 24 | ||
bylo | ||
| √3 |
