ciag arytmetyczny - zadanie tekstowe
Cinu: 1+2+3+...n = 8n
wyznacz n.
S
n =1 + (a
n+1) *4n
S
n = 4n + 4n
2 + 4n
S
n = 4n
2 + 8n
Δ = 2
x
1 = −8 −2 /2 = 5
x
2 = −8 +2 /2 = 3
W odpowiedziach jest n = 15. Pomocy.
20 paź 21:15
Godzio: sprawdź poprawność przejścia 2 linijka −> 3 linijka

20 paź 21:17
Grześ: Źle w ogóle podstawiłeś
| | 1+n | |
Sn= |
| *n i to porównujesz do 8n |
| | 2 | |
20 paź 21:18
Cinu: nie rozumiem.
20 paź 21:21
Grześ: masz ciąg po lewej stronie od 1 do n i tu wyznaczasz sumę ciągu arytmetycznego, 8n po prawej
stronie narazie zostawiasz..
20 paź 21:23
Godzio:
| | a1 + an | |
Sn = |
| * n n−−− to ilość wyrazów a ty masz tych wyrazów n zgoda ? |
| | 2 | |
20 paź 21:23
Grześ: Przecież napisałem to na początku Godzio

20 paź 21:23
Cinu: 8n = n + n
2 /2
16n = n + n
2
−n
2 +15n
x
1 = 0
x
2 = 15
działa

Godzio dlaczego mam zle?
20 paź 21:24
Godzio:
ślepy ostatnio jestem

20 paź 21:24
Godzio: Teraz ok ale wcześniej podstawiłeś za "n" 8n
20 paź 21:24
Grześ: Ja też miałem ostatnio parę pomyłek

20 paź 21:24
Cinu: ok rozumiem juz. Najpierw napisze pozniej pomysle

20 paź 21:25
Cinu: ja mam duzo pomylek ale mam w wiekszosci pomysly na zadania tylko w obliczeniach sie myle
20 paź 21:26
Grześ: zdarza się, ale sam pomysł jest dobry
20 paź 21:27
Godzio:
Ja nie wyspany jestem

20 paź 21:27
Grześ: A mam Godzio takie ciekawe zadanie, ale nie mam pomysłu na nie:
Rozstrzygnij, która z liczb jest większa:
| 1 | |
| 131/2 i tu jest na przemian potęga łańcuchowa w sumie tych potęg jest n |
| 2 | |
i odwrotna kolejność
1/2
1/31/2
Wiesz może jak się za to zabrać

myślałem podstawić jakaś zmienną, ale się nie da chyba

20 paź 21:32
Grześ: Kurde, ja też niewyspany, bo druga potęga miała być w odwrotnej kolejności:
1/31/21/3
20 paź 21:33
Godzio:
| | 1 | | 1 | | 1 | | 1 | | 1 | |
ale |
| tyczy się |
| czy całości: (( |
| )</div> |
| )</div> |
| |
| | 3 | | 2 | | 3 | | 2 | | 3 | |
20 paź 21:35
20 paź 21:35
Grześ: To jest tak, że to po kolei każde jest swoja potęgą
20 paź 21:35
Grześ: Nie da sie tego tu tak dokładnie rozpisać, spróbuje na rysunku narysować
20 paź 21:36
Godzio:
czyli o to może chodzi:
jak to potwierdzisz to już skumam

20 paź 21:37
Grześ:
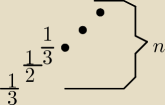
20 paź 21:38
Grześ: I drugi tylko od podstawy 1/2 rusza

20 paź 21:39
Grześ: W każdej jest n potęg
20 paź 21:39
Godzio: no dobra ale do czego dąży to drugie bo tam jest 1/3 1/2 a dalej

?
20 paź 21:40
Grześ: znowu 1/3
20 paź 21:41
Grześ: I tak w kółko
20 paź 21:41
Godzio: aa rozumiem teraz
hmmm

20 paź 21:44
Grześ: Dokładnie, trzeba rozstrzygnąć, która jest większa

, nie można podstawić jakiejś zmiennej, bo
każda potęga jest potęgowana

20 paź 21:48
Grześ: masz jakiś pomysł
Godzio
Widziałem, że wymiatasz tu na forum to się spytałem o takie
zadanko

20 paź 21:51
Godzio: w tym zadaniu nie mam pojęcia jak to ruszyć

20 paź 21:52
Grześ: Mam jeszcze takie skomplikowane równanie kwadratowe z trygonometrią. Nie chcę rozwiązania, broń
Boże, tylko jakieś naprowadzenie:
| | 2π | | 2π | |
cos2x+cos2(x+ |
| )+cosx*cos(x+ |
| )=3/4 |
| | 3 | | 3 | |
Grupować to jakoś czy jak

Chyba najlepiej zmienne wprowadzić i kombinować, tak

20 paź 21:56
Godzio: Można jakoś tak próbować:
| | 1 | | 1 | |
( |
| )1/31/2... = ( |
| )m |
| | 2 | | 2 | |
20 paź 21:57
Grześ: Tylko, że wtedy do tej drugiej liczby nie uda się podstawić, bo np. jak tu ostatnią potęgą
będzie 1/2, to tam 1/3... Myślałem nad tym

20 paź 21:59
Godzio:
| | 2π | | 2π | | 2π | | 3 | |
cos2x + 2cosx * cos(x + |
| ) + cos2(x + |
| ) − cosx * cos(x + |
| ) = |
| |
| | 3 | | 3 | | 3 | | 4 | |
| | 2π | | 2π | | 3 | |
(cosx + cos(x + |
| ))2 − cosx * cos(x + |
| ) = |
| |
| | 3 | | 3 | | 4 | |
i dalej już się chyba leci

ale zaraz sprawdzę na kartce
20 paź 22:00
Jack:
a= {1/3
1\2}
1\3... ⇒ log
1/3 a = {1/2}}
1/3...
b={1\2}
1\3}
1\3...
log
1/3a =b ⇒ 1\3
b=a
Teraz trzeba określić a względem b, ale to juz proste

20 paź 22:01
Grześ: Uuuuu Jack, pięknie, tyle podpowiedzi mi wystarczy, jutro usiądę nad nimi

Nie zauważyłem, że można użyć logarytmu

20 paź 22:04
Grześ: No to Jack wynika z tego, że b jest mniejsze od a

20 paź 22:05
Jack:
 Godzio
Godzio w zasadzie też był bardzo blisko..
20 paź 22:06
Grześ: Bo to będzie funkcja wykładnicza malejąca, dobrze mówie


20 paź 22:07
Jack:
dokladnie tak. Własnie to pisałem...
20 paź 22:08
Grześ: aaaa, to wtedy a będzie mniejsza, fakt, fakt

20 paź 22:08
Grześ: 
Dzięki za pomysł, nie wpadłbym na to

20 paź 22:08
kiko:
A czy nie można zamienić tego zgodnie ze wzorem abc = ab*c
1312*13*12*13*12*13*....
20 paź 22:09
Jack:

Oczywiście trzeba pamiętać, że a,b>0 co widać z tej łańcuchowej potęgi.
20 paź 22:09
Jack:
nie mozna bo ten wzór który napisałaś\eś jest nieprawdziwy.
20 paź 22:10
Grześ: Tylko, żę to c odnosi się wtedy kiko do całości, a nie do b....
20 paź 22:11


 Godzio dlaczego mam zle?
Godzio dlaczego mam zle?




 myślałem podstawić jakaś zmienną, ale się nie da chyba
myślałem podstawić jakaś zmienną, ale się nie da chyba 

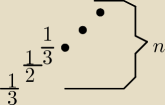

 ?
?

 , nie można podstawić jakiejś zmiennej, bo
każda potęga jest potęgowana
, nie można podstawić jakiejś zmiennej, bo
każda potęga jest potęgowana 
 Widziałem, że wymiatasz tu na forum to się spytałem o takie
zadanko
Widziałem, że wymiatasz tu na forum to się spytałem o takie
zadanko 

 Chyba najlepiej zmienne wprowadzić i kombinować, tak
Chyba najlepiej zmienne wprowadzić i kombinować, tak

 ale zaraz sprawdzę na kartce
ale zaraz sprawdzę na kartce

 Nie zauważyłem, że można użyć logarytmu
Nie zauważyłem, że można użyć logarytmu 

 Godzio w zasadzie też był bardzo blisko..
Godzio w zasadzie też był bardzo blisko..



 Dzięki za pomysł, nie wpadłbym na to
Dzięki za pomysł, nie wpadłbym na to 
 Oczywiście trzeba pamiętać, że a,b>0 co widać z tej łańcuchowej potęgi.
Oczywiście trzeba pamiętać, że a,b>0 co widać z tej łańcuchowej potęgi.