Mam problem, proszę o podpowiedzi! Camillo: |x²−2x|<x czy rozłożyć to na : |x*(x−2)|<x ? jesli tak to co dalej?

Grześ: Było takie zadanie rozwiązywane na forum niedawno, poszukam go.

Grześ: Nie mogę znaleźć, ale osoby z forum będą pamiętać.

Camillo: podbijam

Grześ: Pamiętam tylko to, że na forum rozważali to sposobem graficznym, czyli że najpierw rysujemy funkcje f(x)=|x²−2x| oraz g(x)=x i zaznaczyć miejsce, gdzie funkcja f(x)ma mniejszą wartość od g(x)

ce es: |x²−2x|<x x²−2x<x lub −x²+2x<x x²−3x<0 lub −x²+x<0 x(x−3)<0 lub x(1−x)<0 to juz chyba rozwiązesz

ce es: −x2+2x>x zapomniałem zmienić znak nierówności na przeciwny

Godzio: 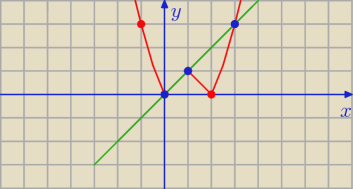f(x) = |x² − 2x| g(x) = x Odp: x ∊ (−1,3)

Godzio: ce es tak niestety nie można zrobić trzeba rozpatrywać przypadki 1^o x ∊ (−∞,0) 2^o x ∊ <0,2) 3^o x ∊ <2,∞)

Camillo: czyli w końcu jak ma byc?

Godzio: albo wykres albo rozwiązuj w tych przedziałach co CI rozpisałem

Camillo: No tak, ogoleni to juz predzej robilem w tych przedzialach ale cos mi nie wyszlo, bo nie zgadza sie z odpowiedzia

Godzio: Pokaż obliczenia to poszuka się błędu Co do mojej odp, to oczywiście powinno być x ∊ (1,3)

Godzio: Dobra zlituję się, nudy są to mogę napisać |x² − 2x| < x |x| * |x − 2| < x 1^o x ∊ (−∞,0) |x| = −x, |x − 2| = −x + 2 −x(−x + 2) < x x² − 2x < x x² − 3x < 0 x(x − 3) < 0 ⇒ x ∊(0,3) ⇒ brak rozwiązań w danym przedziale 2^o x ∊ <0,2) |x| = x, |x − 2| = −x + 2 x(−x + 2) < x −x² + 2x < x x² − x > 0 x(x − 1) > 0 ⇒ x ∊ (−∞,0) ∪ (1,∞) ⇒ x ∊(1,2) 3^o x ∊ <2,∞) |x| = x, |x − 2| = x − 2 x(x − 2) < x x² − 2x < x x² − 3x < 0 x(x − 3) < 0 ⇒ x ∊ (0,3) ⇒ x ∊ <2,3) Odp: x ∊ (1,3)

ce es: wyszlo Ci Godzio tak samo jak mi, zaluje Ciebie

Godzio: to nie znaczy że wykonanie jest poprawne Twoje rozwiązania nie wyklucza początkowo że x < 0 −− a właśnie dla takiego x jest to sprzeczność