a
nick: W trapezie ABCD ramiona AD i BC przedłużono tak, że przecięł się w punkcie . Oblicz długość
odcinka MD, jeżeli AD=21 cm, AB=48cm, CD=36cm.
18 paź 12:22
anies: proponuję powtórzyć twierdzenie talesa
i policz
pzdr.
18 paź 13:29
Nadek:
Spróbój zweryfikować poprawność moich sposobów "przedpotopowym"
Talesem.Ja bym rozwiązał układ równań:
| MD | | 36 | | MD + 21 | | 48 | |
| = |
| & |
| = |
| & sinC = sinB |
| sinC | | sinM | | sinB | | sinM | |
18 paź 13:37
nick: w życiu tego nie rozwiąże... masakra. może mi to ktoś zrobić?
18 paź 13:47
Godzio:
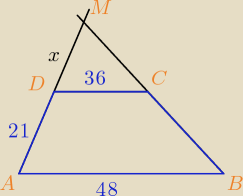
Z podobieństwa trójkątów: ΔDCM ~ ΔABM mamy proporcję:
| bok trójkąta DCM | | podstawa trójkąta DCM | |
| = |
| = |
| bok trójkąta ABM | | podstawa trójkąta ABM | |
| x | | 36 | |
| = |
| −−− mnożę "na krzyż" |
| 21 + x | | 48 | |
48x = 36 * 21 + 36x / − 36x
12x = 36 * 21 /:12
| | 36 * 21 | |
x = |
| = 3 * 21 = 63 cm |
| | 12 | |
18 paź 13:59