Narysować wykres funkcji Zielonooka19: Wykres funkcji: Czy mógłby mi ktoś wyjaśnić, jak narysowac wykres takiej funkcji:

	1
f(x) = |		|
	(x+1)2 − 3

	1
wiem, jak wygląda wykres dla		, ale co się dzieje przy tej trójce? Bo później
	(x+1)2

wartość bezwzględną też spokojnie zrobię. Tylko to jedno miejsce.. Będę wdzięczna!

sushi_ gg6397228: "−3" ma byc w mianowniku czy za kreska ułamkowa

Zielonooka19: w mianowniku, jak widać

sushi_ gg6397228: ja bym zrobil tak

	1
(x+1)2−3= x2 +2x−2 policzyl delte dwa miejsca zerowe i zrobil wykres jak dla
	x2

podstawiajac wczesniej kilka charakterystycznych punktów

Zielonooka19: i nie bardzo wiem dalej... może ma ktoś inne pomysły?

Jack: Zależy czym dysponujesz... Ale można tak: Na początek zrób bez modułu. Zbadaj dziedzinę, policz granice obustronne w punktach wyrzuconych z dziedziny (wyjdą asymptoty), policz granice przy x→±∞, wykonaj wykres i na koniec odbij od OX.

Ewa: −3 oznacza przesunięcie wykresu o trzy jednostki w prawo na osi x

Jack: na pewno nie. Przesunięcie musi rosnąć z taką samą potęgę jak zwykły x. To znaczy z kwadratem. Za przesunięcie odpowiada +1 w nawiasie. Poza tym, przez −3 pojawiają się punkty które należy wyrzucić z dziedziny... Przez zwykłe przesunięcie czegoś takiego by nie było.

Zielonooka19: Dysponuję podstawową matematyką i szybko próbuje nadrobić.. Zaraz spróbuję tak jak mówiłeś, może coś wyjdzie..

Jack: ciężko może być z samą podstawą...ale spróbuj.

Zielonooka19: Jeśli chodzi o dziedzinę −> potrafię aż wyliczyć deltę i miejsca zerowe. I dalej nie wiem co robić.

Jack: no właśnie, może jesli tylko się uczysz i dopiero stawiasz pierwsze kroki, daruj sobie to zadanie... Jesli bardzo chcesz... to pomyslimy dalej.

Zielonooka19: Bardzo chcę − muszę się nauczyć jeśli chce zaliczyć semestr i zrobić zadanie domowe. Po cichu liczę, że takiego aż czegoś na kolokwium nie trafię − robiłam kilkadziesiąt innych przypadków ale ten mnie przerósł

Jack:

	1
f(x)=
	(x+1)2−3

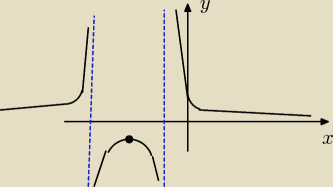
1. D:R\{√3−1,−√3−1} 2.

	1
limx→√3−1+		=+∞
	(x+1)2−3

	1
limx→√3−1−		=−∞
	(x+1)2−3

	1
limx→−√3−1+		=−∞
	(x+1)2−3

	1
limx→−√3−1−		=+∞
	(x+1)2−3

3.

	1
limx→∞		=0
	(x+1)2−3

	1
limx→−∞		=0
	(x+1)2−3

	1		2x+2
4. f'(x)=(		)'=−		⇒ f'(x)=0 ⇔ x=−1
	(x+1)2−3		((x+1)2−3)2

ponadto w otoczeniu punktu −1 nastepuje zmiana znaku z " + " na " − ", czyli mamy maksimum. f(−1)=−1/2 TERAZ ROBIMY WYKRES

Jack: mam nadzieję że się nie walnąłem w rachunkach

Zielonooka19: Czyli ja nie wiem nic o "lim"... Czyli nie wiem nic xD

Jack: ups... tak podejrzewałem. No nic, a mówiłem żeby zostawić zadanie

Zielonooka19: Myślę, że nauczyciel sie zlituje i wyjaśni. Wybacz, że Ci tyleee czasu zabrałam i bez sensu bo mało wiem z tego

Jack: nie przejmuj się Powodzenia!

Zielonooka19: