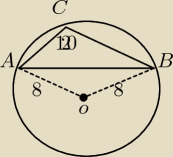
 Uwzględniając dane na rysunku oblicz pole trójkąta ABC.
Uwzględniając dane na rysunku oblicz pole trójkąta ABC.
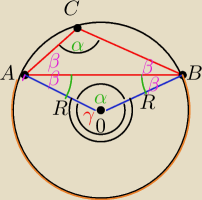 α=120o
γ=240o
β=30o
R=8
W trójkacie równoramiennym AOB kąt AOB ma miare α= 120o
Kąt BAO i kąt ABO mają miare β=30o
Suma kątów wewnętrznych czworokąta wynosi 360o
Więc żeby obliczyc pole tróójkąta ABC przy tych danych zostaje tylko jedna mozliwośc
Pole trójkata ABC musi byc równe polu trójkata AOB więc kąty CAB i CBA ich miary wynosza po
30o
czyli tez to musi byś trójkat równoramienny o ramionach R=8 i kątach przy podstawie po 30o
Innej mozliwowsci nie ma . Zrobiłem rysunek (narysowałem dwa trójkaty ABC o kacie
wierzcholkowym 120o i w jednym trójkącie katy przy podstawie miały mare 15o i 45o w drugim
25o i 35o )
Pola tych trójkątów sie rózniły Wię przy tych danych nie ma możliwości policzyć (brakuje albo
kąta albo długości któregoś ramienia
PABC= 2*R2*sinβ*sinβ*sinα
α=120o
γ=240o
β=30o
R=8
W trójkacie równoramiennym AOB kąt AOB ma miare α= 120o
Kąt BAO i kąt ABO mają miare β=30o
Suma kątów wewnętrznych czworokąta wynosi 360o
Więc żeby obliczyc pole tróójkąta ABC przy tych danych zostaje tylko jedna mozliwośc
Pole trójkata ABC musi byc równe polu trójkata AOB więc kąty CAB i CBA ich miary wynosza po
30o
czyli tez to musi byś trójkat równoramienny o ramionach R=8 i kątach przy podstawie po 30o
Innej mozliwowsci nie ma . Zrobiłem rysunek (narysowałem dwa trójkaty ABC o kacie
wierzcholkowym 120o i w jednym trójkącie katy przy podstawie miały mare 15o i 45o w drugim
25o i 35o )
Pola tych trójkątów sie rózniły Wię przy tych danych nie ma możliwości policzyć (brakuje albo
kąta albo długości któregoś ramienia
PABC= 2*R2*sinβ*sinβ*sinα
| 1 | 1 | √3 | ||||
PABC=2*82* | * | * | ||||
| 2 | 2 | 2 |
| 32√3 | ||
PABC= | =16√3 | |
| 2 |
 ?
?
