Jak obiecalem zadanie dla Licealistow :) Tomek.Noah: √2^x−1+1≥|2^x−1−1|+2^xlog_x√x moj wynik jak i w ksiazce to x∊(0,1)∪(1,log₂5−1) no Godzio do roboty i jak sprawdzales zadania z AGH'u?

Tomek.Noah: Oczywiscie kazdy moze spróbować swoich sil i napisac swoje zdanie jest to jakby zadnaie zbiorowe

Godzio: dobra, zabieram sie a te zadania z AGH to mam rozwiązane dam Ci odp a ty tylko byś potwierdził ok ?

Tomek.Noah: ok

Godzio: x > 0, x ≠ 1 D = (0,1)∪(1,∞) 1^o 2^{x − 1} − 1 < 0 ⇒ 2^{x − 1} < 1 ⇒ x − 1 < 0 ⇒ x < 1 dla x ∊(0,1) √2^{x − 1} + 1 ≥ −2^{x − 1} + 1 + 2^x * log_x√x

	1
√2x − 1 + 1 ≥ −2x − 1 + 1 + 2x *
	2

√2^{x − 1} + 1 ≥ −2^{x − 1} + 1 + 2^{x − 1} √2^{x − 1} + 1 ≥ 1 /² 2^{x − 1} + 1 > 0 2^{x − 1} + 1 ≥ 1 2^{x − 1} ≥ 0 x ∊ R ⇒ Odp: x ∊(0,1) 2^o 2^{x − 1} − 1 > 0 ⇒ 2^{x − 1} > 1 ⇒ x − 1 > 0 ⇒ x > 1 dla x ∊(1,∞)

	1
√2x − 1 + 1 ≥ −2x − 1 + 1 + 2x *
	2

√2^{x − 1} + 1 ≥ 2^{x − 1} − 1 + 2^{x − 1} 2^{x − 1} = t , t > 0 √t + 1 ≥ 2t − 1 /² −−−− 2^t − 1 jest zawsze dodatnie dla danego x t + 1 ≥ 4t² − 4t + 1 4t² − 5t ≤ 0 / : t 4t − 5 ≤ 0

	5
t ≤
	4

1		5
	* 2x ≤
2		4

	5
2x ≤
	2

	5
Odp: x ∊ (1,log2		>
	2

	5
Odp: (0,1) ∪(1,log2		>
	2

Tomek.Noah: mi same pisanie a gdzie robilem plynnie zajelo mi 5−10 min a ty na kompie 2 minut cos krecisz haha

Tomek.Noah: no niby dobrze ale ja mam calkiem inne rozwiazanie i nie onbraz sie logiczne wyaje mi sie ze twoje tez jest dobrze

Tomek.Noah: ale wydaje mi sie ze troche opusciles przeksztalcen dosc istotnych

Tomek.Noah: dobra dawaj te odpowiedzi z AGH

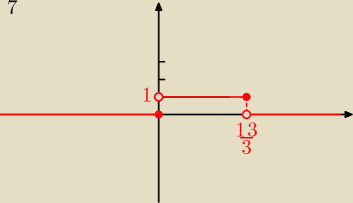
Godzio: Coś takiego mi nawychodziło:

	R		(√3 + 1)(√2 + 1)
zad. 1:		=
	r		2

zad. 2: Jest jedna parzysta

	23√2 − 1
zad. 3: p =
	5

zad. 4: C(1,0)

	1
zad. 5: √a + 1 =		* (2 * 10n + 1)
	3

2 * 10ⁿ + 1 jest podzielne przez 3 ponieważ suma cyfr jest równa 3 więc jest to liczba naturalna zad. 6: Rozwiązaniem będzie tylko dziedzina tylko wnętrze okręgu stanowiące część wspólną z parabolą bez y = 1 zad. 7 x < 0

Godzio: A Tobie jak w ogóle wyszło w tym zadaniu ?

Godzio: w 3. miało być

23√3 − 1
5

Tomek.Noah: moje odpoweidzi ale moje juz byly oceniane i sa dobrze wiec szok dla Ciebie moj dorgi 1)2+√3 2) jedna parzysta ppn 3) p=1 4)c(1,4) v c(1,0) 5tak samo 6nie pamietam 7 to jest tak:

	64		64		64
g(m)={0 m∊(		, +∞) &1 m∊(−∞,0>u{		} &2 m∊(0;		)
	9		9		9

Tomek.Noah: ok ja lece jak chcesz postatram sie jutro napisac ci moje rozwiazania ok?

Godzio: o cholipka w sumie w 4 mi tak samo wyszło ale stwierdziłem że to drugie trzeba odrzucić nie wiem czemu

Godzio: ok, poszukam jeszcze błędów