 |x − 2| − |x − 1| − |x + 1| + 5 > 0
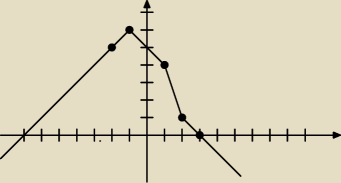
f(x) = |x − 2| − |x − 1| − |x + 1| + 5
punkty w których poszczególne wartości bezwzględne się zerują:
x − 2 = 0 → x = 2
x − 1 = 0 → x = 1
x + 1 = 0 → x = −1
f(−2) = |−2 − 2| − | −2 − 1| − |−2 + 1| + 5 = 4 − 3 − 1 + 5 = 5
f(−1) = 3 − 2 + 5 = 6
f(1) = 1 − 2 + 5 = 4
f(2) = −1 − 3 + 5 = 1
f(3) = 1 − 2 − 4 + 5 = 0
robimy sprawdzenie czy rzeczywiście dla −7 wychodzi 0
f(−7) = 9 − 8 − 6 + 5 = 0
czyli dla x∊(−7,3) wartości funkcji są dodatnie.
|x − 2| − |x − 1| − |x + 1| + 5 > 0
f(x) = |x − 2| − |x − 1| − |x + 1| + 5
punkty w których poszczególne wartości bezwzględne się zerują:
x − 2 = 0 → x = 2
x − 1 = 0 → x = 1
x + 1 = 0 → x = −1
f(−2) = |−2 − 2| − | −2 − 1| − |−2 + 1| + 5 = 4 − 3 − 1 + 5 = 5
f(−1) = 3 − 2 + 5 = 6
f(1) = 1 − 2 + 5 = 4
f(2) = −1 − 3 + 5 = 1
f(3) = 1 − 2 − 4 + 5 = 0
robimy sprawdzenie czy rzeczywiście dla −7 wychodzi 0
f(−7) = 9 − 8 − 6 + 5 = 0
czyli dla x∊(−7,3) wartości funkcji są dodatnie.