parametr m jabłko: Oblicz dla jakich wartości parametru m funkcja określona wzorem f(x)=(m−4)x²−4x+m−3 ma dwa miejsca zerowe, z których jedno jest mniejsze od 1 a drugie większe od 1. 1. Δ>0 −4m²+28m−32>0 i co dalej?

Godzio: naszkicuj sobie tą sytuację i zobacz jaki musi być warunek żeby tak było

jabłko: tzn że m może być każdą liczbą rzeczywistą \{1}?

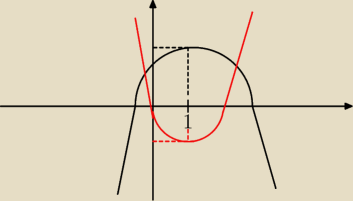
Godzio: 1^o Δ > 0 f(1) > 0 a < 0 Odp: część wspólna 2^o Δ > 0 f(1) < 0 a > 0 Odp: część wspólna Odp końcowa: suma rozwiązań z obu przypadków

jabłko: spoko, rozumie tzn nie do końca.. dlaczego/ w jakim celu jest to drugie założenie że f(1)>0 no i w drugim przypadku że f(1)<0 ?

jabłko: *rozumiem

Godzio: bo jeśli te warunki nie będą spełnione to zauważ że miejsca zerowe albo będą większe od jedynki albo mniejsze i nie koniecznie jedno będzie musiało być większe a drugie mniejsze od 1

jabłko: tzn. chodzi o to ze gdy wierzchołek funkcji będzie w x=1 to nie ma możliwości by było yam miejsce zerowe, tak?