zadania Karolina: Zad. 1. W trójkącie ABC punkty S i T są odpowiednio środkami boków AC i AB. Odcinki BS i CT są prostopadłe i mają długości odpowiednio 8 cm i 12 cm. Jakie jest pole trójkąta? Zad. 2. Niech [a] oznacza część całkowitą, a {a} − część ułamkową liczby a. Rozwiąż w liczbach dodatnich układ równań z trzema niewiadomymi: x + [y] + {z} = 4,2, y + [z] + {x} = 3,6, z + [x] + {y} = 2,0. Zad. 3. Czworokąt jest ograniczony liniami o równaniach: x=0, x=4, 4y=3x+8 i y=k, gdzie k<2. Dla jakiej wartości k wartości liczbowe obwodu i pola tego czworokąta są jednakowe?

Radosław: Zad 1 P=¹₂|AB||AC|=¹₂[(12−x)(8−y) + (8−y)x +(12−x)y +xy] + ¹₈|AB||AC| ={1}{4}P P={2}{3}96=64

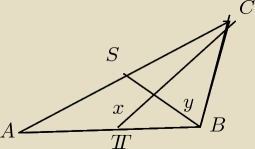
Radosław: Zad1 P=¹₂|AB||AC|sinA =¹₂[(12−x)(8−y) + (8−y)x + (12−x)y + xy] + [¹₈|AB||AC|sinA] P=²₃96 = 64 P.S. Poprawiam bo w pierwotnym zapisie pozjadałem niektóre znaki ¹₈|AB||AC|sinA =¹₄P