Dwa okręgi są styczne w punkcie S. michal: Dwa okręgi są styczne w punkcie S. Przez ten punkt poprowadzono proste KL i MN, odpowiednio przecinające pierwszy okrąg w punktach K i M, a drugi w L i N. Udowodnij, że KM || LN.

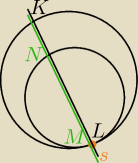
l: sNMLMN Wydaje mi się ze tak to wyglada. zeby pierwszy okrąg został przecięty w punktach K i M, a drugi w L i N, proste KM i LN muszą na siebie nachodzić czyli są równoległe.

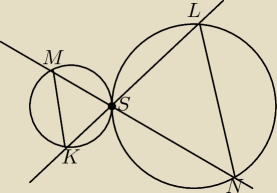
Vax: Rozważmy jednokładność o środku w punkcie S, przekształcającą okrąg na którym znajdują się punkty K,L na drugi. Wtedy j(K) = L , j(M) = N, ale dwa punkty jednoznacznie wyznaczają prostą, więc prosta MK w danej jednokładności przejdzie na NL, a proste w jednokładności przechodzą na proste równoległe qed.