równania i nierówności kwadratowe pomóżcie :): dla jakich wartości parametrum równanie Ix³ − 9I + Ix² − 16I =m ma dokładnie dwa różne pierwiastki?

Godzio: maźnij wykresik tego co po lewej jest i zobacz kiedy prosta m przetnie wykres dokładnie 2 razy

pomóżcie :): ale własnie niew iem jak maznac ten wykres..

Godzio: no nie będzie do za proste ale może coś wymyśle rozumiem że jesteś II LO ?

pomóżcie :): jestem w III i powtarzam materiał z I i nic nie poamietam a to praca domowa

pomóżcie :): pomylka tam jest Ix² − 9I przepraszam

Godzio: Zapytałem właśnie dlatego że tam było x³ ale skoro tak to banał, zaraz Ci to rozrysuje

pomóżcie :): wpierw robie x≥0 potem x<o delta pierwiastki wierzcholek paraboli? dobrze?

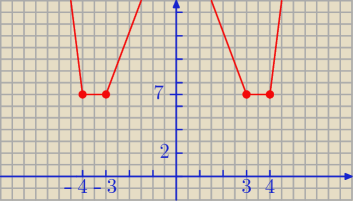
Godzio: x² − 9 ≥ 0 ⇒ x³ ≥ 9 ⇒ x∊(−∞,−3>∪<3,∞) ⇒ |x² − 9| = x² − 9 x² − 9 < 0 ⇒ x³ < 9 ⇒ x ∊(−3,3) ⇒ |x² − 9| = − x² + 9 x² − 16 ≥ 0 ⇒ x∊(−∞,−4>∪<4,∞) ⇒ |x² − 16| = x² − 16 x² − 16 < 0 ⇒ x∊(−4,4) ⇒ |x² − 16| = −x² + 16 1^o x∊(−∞,−4>∪<4,∞) f(x) = x² − 9 + x² − 16 = 2x² − 25 2^o x ∊ (−4,−3>∪ <3,4) f(x) = x² − 9 − x² + 16 = 7 3^o x ∊ (−3,3) f(x) = −x² + 9 − x² + 16 = −2x² + 25 najwyższy punkt to 25 więc 2 rozwiązania są dla m ∊ (25,∞)

pomóżcie :): dziekuje1 w takim raziem moze pestka beda dla ciebie moje pozostale dwazadanka ktore umiescilam niedawno. widze ze nikt niemoze ich rozgryzc. pod nickiem tym samym