Korzystając z wzoru cosinusów wykaż smmileey:

	a2+b2		1
Korzystając z wzoru cosinusów wykaż, że		=		, gdzie a i b są
	d12+d22		2

długościami boków równoległoboku oraz d1 i d2 są długościami jego przekątnych.

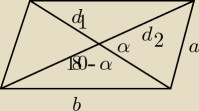
Godzio: cos(180 − α) = −cosα

	1		1		d1		d2
b2 = (		d1)2 + (		d2)2 − 2		*		cos(180 − α)
	2		2		2		2

	1		1		d1d2
b2 =		d12 +		d22 +		cosα
	4		4		2

	1		1		d1		d2
a2 = (		d1)2 + (		d2)2 − 2		*		cosα
	2		2		2		2

	1		1		d1d2
a2 =		d12 +		d22 −		cosα
	4		4		2

dodaje równania:

	1		1
a2 + b2 =		d12 +		d2
	2		2

	1
a2 + b2 =		(d12 + d22)
	2

a2 + b2		1
	=
d12 + d22		2

Eta: oznaczam dla ułatwienia zapisu e, f −− dł. przekątnych ze wzoru cosinusów mamy e²= a² +b² −2ab *cosα f²= a² +b² −2ab *cos( 180^o−α) ....... cos(180^o−α) = − cosα e² = a²+b² −2ab cosα f²= a²+b² +2ab cosα −−−−−−−−−−−−−−−−−−−−−− e²+f²= 2a² +2b² e²+f²= 2( a²+b²) to :

	a2+b2		1
		=
	e2+f2		2

c. n.u

Eta: Godzio ......... wiesz? ..... co powiedziałby na to Gustlik

Bogdan: Nie tylko Gustlik

smmileey: Dziękuję.

sa: coto sa za wzory? Bo nie tak probuje znalezc sens w tym rozwiazanie i nie potrafie

sushi_ gg6397228: wzory: twierdzenie cosinusów

sa: no znalazem juz. Jednak wciaz nie moge zrozumiedc zapisow Godzia. Po czym mozna wywnioskowac , ze tak wlasnie powinien wygladac rysunek?

sushi_ gg6397228: rownoleglobok chyba wiesz co to jest, w zadniu jest podane: boki "a,b", przekatne "d₁,d₂"

sa: Czyli rozumiem ,ze sugerowal sie oznaczeniem , ktore jest takze uzywane dla rownoleglobokow?

sushi_ gg6397228: nie po to zrobil rysunek i dal oznaczenia, aby potem sobie litery i liczby z kosmosu podstawiał przeciez w pierwszym poscie zostalo wyjasnione, co oznaczaja kazde literki

sa: a fakt nie doczytalem do konca. Juz rozumiem wszystko. dzieki za pomoc