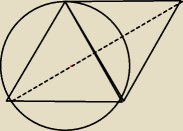
geometria pole rombu lemurek: Okrąg przechodzący przez wierzchołek kąta ostrego rombu i wierzchołki kątków rozwartych tego rombu dzieli przekątną rombu na dwa odcinki długości 17 cm i 8 cm. Oblicz pole rombu Niestety nie wiem co tutaj zrobić R=8,5, do tego doszedłem, ale nie wiem jak później obliczy długości przekątnych

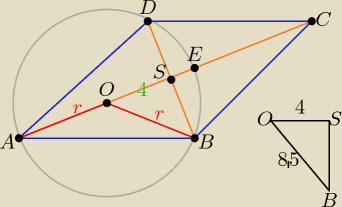Bogdan: |AE| = 17, |EC| = 8, |AO| + |OE| = 17, |AO| = |OE| = |OB| = r = 8,5 |AC| = 17 + 8 = 25, |AS| = |SC| = 12,5, |SE| = 12,5 − 8 = 4,5, |OS| = 8,5 − 4,5 = 4 |BS|² = r² − |OS|² = 8,5² − 4² = 56,25 ⇒ |BS| = 7,5, |BD| = 2 * 7,5 = 15

	1
Pole rombu P =		* |AC| * |BD|
	2

lemurek: Wielkie dzięki, jednak dokładny rysunek faktycznie bardzo pomaga

Mati: Mam pytanie . Skąd wiemy że punkt O leży na prostej AC ?

Basia: okrąg jest opisany na trójkącie równoramiennym BAD AS zawarty w AC jest jego wysokością, dwusieczną, środkową i symetralną OB = OD = r ⇒ O∊ sym.BD = pr.AC −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Bogdanie dlaczego OS = 4 ? moim zdaniem to BS = 4 OS² + 4² = (8,5)²