A A: Parę zadań na poziom rozszerzony Jedna uwaga − zadania są na poziomie "starej" matury z matematyki, także niektóre zagadnienia zawarte w tych zadaniach mogą nie obowiązywać. Niemniej jednak warto rozwiązać 1. Rozwiąż równanie 2^sin2x + 2^cos2x = 3

A:

	n+1 2
2. Wykaż, że n3 ≥		dla każdego n∊N

3. Dla jakich wartości x szereg geometryczny x − x³ + x⁵ − x⁷ +.... jest zbieżny? Wykreśl sumę tego szeregu jako funkcję zmiennej x.

	5
4. Oblicz dokładnie wartość: a) sin75 b) cos		π
	12

5. W równoległoboku o polu 72cm² przekątne mają długość 20 i 12 cm. Oblicz długość dłuższego boku tego równoległoboku. 6. Rozwiąż nierówność x⁴ − 6x³ + 3x² + 26x − 24 ≤ 0 7. Wyznacz wszystkie wartości parametru m tak, aby równanie (2m+1)x² − (m+3)x + 2m +1 = 0 miało dwa różne pierwiastki x₁,x₂ spełniające warunek x₁²(1+x₂) + x²(1+x₁) > −2 8. Dane są punkty: A=(1,2,3), B=(4,3,3), C=(3,6,3), D=(0,5,3), W=(2,4,−7) Sprawdź, czy ostrosłup o podstawie ABCD i wierzchołku W jest ostrosłupem prawidłowym. Oblicz objętość tego ostrosłupa.

A: 9. Trójkąt prostokątny o przyprostokątnych 6cm i 8cm obraca się dokoła prostej zawierającej przeciwprostokątną. Oblicz objętość i pole powierzchni powstałej bryły 10. Z urny pierwszej przenosimy jedną kulę do drugiej urny. Następnie z drugiej urny losujemy jedną kulę. Jaka jest szansa, że w pierwszym losowaniu pobrano kulę białą, jeśli wiadomo, że w drugim losowaniu wyciągnięto kulę czarną?

	π		π
11. Naszkicuj wykres funkcji f(x) = sin(|x−		| + x −		)
	2		2

A: Adnotacja do zadania 10. W pierwszej urnie mamy 3 kule białe i 2 czarne. W drugiej urnie mamy jedną kulę białą i 4 czarne.

Kejt: to ja się połaszę na 9. można tutaj rozwiązanie podać? ;>

Jack: 1. podstawienie t=2^sin2x, t>0 t=2^sin2x t=2^1−cos2x

	2
2cos2x=		, t≠0
	t

Stąd,

	2
t+		=3
	t

t²−3t+2=0 t₁=1 t₂=2 dla t=1 1=2^sin2x 2⁰=2^sin2x 0=sin²x x= kπ, k∊Z (całkowite) dla t=2 2=2^sin2x 2¹=2^sin2 1=sin²x

	π
x=		+kπ , k∊Z
	2

	πk
Ostatecznie x=		, gdzie k∊Z.
	2

Ломоно́сов: 10. Wprowadźmy oznaczenia: A − zdarzenie polegające na wylosowaniu kuli czarnej z drugiej urny B₁ − zdarzenie polegające na przeniesieniu kuli białej z pierwszej urny do drugiej B₂ − zdarzenie polegające na przeniesieniu kuli czarnej z pierwszej urny do drugiej Przeniesienie danej kuli jest równoznaczne z jej wylosowaniem. Skoro w pierwszej urnie mamy łącznie 5 kul, to:

	3
P(B1) =		( losujemy jedną białą kulę spośród trzech dostępnych białych)
	5

	2
P(B2)=		(losujemy jedną czarną kulę spośród dwóch dostępnych czarnych)
	5

Aby obliczyć P(A) należy skorzystać z wzoru na prawdopodobieństwo całkowite P(A) = P(A/B₁) * P(B₁) + P(A/B₂) * P(B₂) W naszym przypadku: P(A/B₁) − prawdopodobieństwo, że wylosujemy z drugiej urny kulę czarną pod warunkiem, że z pierwszej urny wylosowaliśmy kulę białą. P(A/B₂) − prawdopodobieństwo, że wylosujemy z drugiej urny kulę czarną pod warunkiem że z pierwszej urny wylosowaliśmy kulę czarną. P(A/B₁) − w drugiej urnie mamy 6 kul − 4 czarne i 2 białe (łącznie z pobraną białą).

	4
P(A/B1) =
	6

P(A/B₂) − w drugiej urnie mamy 6 kul − 5 czarnych i jedną białą (łącznie z pobraną czarną)

	5
P(A/B2) =
	6

	4		3		5		2		22
P(A) =		*		+		*		=
	6		5		6		5		30

Musimy jeszcze obliczyć prawdopodobieństwo wylosowania z pierwszej urny kuli białej pod warunkiem, że z drugiej urny wylosowano kulę czarną ⇒ P(B₁/A) Wynik doświadczenia jest nam znany − wylosowanie kuli czarnej. Korzystamy zatem ze wzoru Bayesa

	4		3		30		6
P(B1/A) =		*		*		=		− co jest poszukiwaną szansą
	6		5		22		11

Kejt:

8*6		10*h
	=
2		2

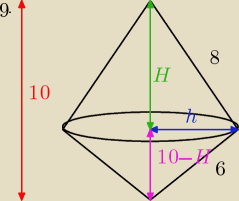
8*6=10h 48=10h h=4,8 H²=8²−h² H²=64−23,04 H²=40,96 H=6,4 V_c=V₁+V₂

	1
V=		πr2H
	3

	1
V1=		* π * 23,04 * 6,4
	3

V₁=49,152π

	1
V2=		* π * 23,04 * 3,6
	3

V₂=27,648π V_c=49,152π+27,648π=76,8π≈241,152 (nie wiem czy trzeba przybliżyć..ale na wszelki wypadek ) P_bc=P_b1+P_b1 P_b=πrl P₁=π4,8*8=38,4π P₂=π4,8*6=28,8π P_bc=38,4π+28,8π=67,2π≈211,008 (tutaj też nie wiem..) mam nadzieję, że dobrze wyszło

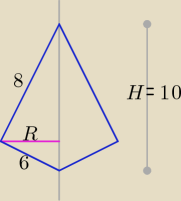
Bogdan: Zadanie 9.

	8 * 6		48
R =		=		= 4,8
	10		10

	1		1
V =		πR2H =		π*4,82*10 = 76,8π
	3		3

P = πR*8 + πR*6 = 14πR = 14*4,8π = 67,2π