Próbna matura z "Gazetą Wyborczą" Ломоно́сов: Dzisiaj do "Gazety Wyborczej" został dołączony próbny arkusz maturalny z matematyki, poziom podstawowy. Zamieszczam przykładowe zadania otwarte, jeżeli ktoś zapomniał kupić, a chciałby porozwiązywać: 1. Obwód prostokąta jest równy 12, a jego pole jest równe 6. Oblicz długości boków tego prostokąta 2. W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość 6 i tworzy z wysokością ostrosłupa kąt o mierze 40 stopni. Oblicz objętość tego ostrosłupa. 3. Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia A − w pierwszym rzucie liczba oczek będzie mniejsza od 4 i iloczyn otrzymanych liczb oczek będzie podzielny przez 4.

	2
4. Kąt α jest ostry i cosα =		. Oblicz 2 + 4tg2α
	3

5. Oblicz najmniejszą i największą wartość funkcji kwadratowej f(x) = x² + 8x −5 w przedziale <−1 ; 0> 6. Wyrazami ciągu arytmetycznego (a_n) są kolejne liczby naturalne, które przy dzieleniu przez 4 dają resztę 3. Ponadto a₂ = 7. Oblicz a₁₀ 7. W układzie współrzędnych na płaszczyźnie punkt S − (−2, 4) jest środkiem okręgu stycznego do osi Oy. Wyznacz równanie tego okręgu.

M4ciek: 4.

	2
cos α =		, 2 + 4tg2 α = ?
	3

	sin2α		1−cos2α		2   1−( )2   3
2+4		= 2 + 4		= 2 + 4		=
	cos2α		cos2α		2   ( )2   3

	5   9		5		9		20
= 2 + 4		= 2 + 4*		*		= 2 +		= 7
	4   9		9		4		4

Jeszcze odpowiedzi podajcie

M4ciek: 5. f(x)= x² + 8x −5 , <−1;0>

	−b
p=
	2a

	−8
p=
	2

p=−4 p∉ <−1;0> f(−1)=1−8−5=−11 f(0)=−5 f_min = f(−1) = −11 f_max = f(0) = −5

Ломоно́сов: Maciek uzyskałeś prawidłową odpowiedź

	4		5		sin2α		5
cos2α =		, stąd sin2α =		, tg2α =		=
	9		9		cos2α		4

	5
2 + 4tg2α = 2 + 4 *		= 7
	4

M4ciek: W zadaniu 1 pole nie powinno byc rowne 8?

Ломоно́сов: Pole jest równe 6. Tak widnieje w treści zadania.

M4ciek: Gra gra teraz juz mialem zapisywac...

M4ciek: 7. S(−2;4) (x−a)²+(y−b)²=r² (x+2)²+(y−4)²=2² (x+2)²+(y−4)²=4 Tak to powinno wygladac?

M4ciek: Widze think wycofala 1. 2a+2b=12/:2 a*b=6 a+b=6 a*b=6 a=6−b (6−b)b=6 −b²+6b−6=0 Δ=36−4*(−1)*(−6) Δ=12 √Δ=√12=2√3

	−6+2√3		−6−2√3
b1=		b2=
	−2		−2

	−2(3−√3)		−2(3+√3)
b1=		b2=
	−2		−2

b₁=3−√3 b₂=3+√3 a₁+b=6 a₂+b=6 a₁+3−√3=6 a₂+3+√3=6 a₁=6−(3−√3) a₂=6−(3+√3) a₁=3+√3 a₂=3−√3

think: bo to było tylko dla Twoich oczu jak by to powiedzieli w jednym takim filmie

M4ciek: A co z tym 7?

M4ciek: a₂=7 a₃=11

a1+a3
	=a2
2

a1+11
	=7
2

a₁+11=14 a₁=3 a₁₀ = ? a₁₀= a₁ + (n−1)r a₁₀= 3 + (10−1)4 a₁₀= 3 + 36 a₁₀=39

Eta: 6/ takimi liczbami są : 3, 7, 11,....... tworzą ciąg arytmetyczny: a₁= 3 r= 4 a₁₀= a₁ +9r = 3+ 36 = 39

M4ciek: Tak tez mozna Oczywiscie ja z Warszawy do Wroclawia przez Rzeszow

Eta: Maciek, ile to jest : 1 −8 −5 = ? sprawdź co napisałeś w zad. 5

Bogdan: Zad. 6. Korzystamy z zależności dla ciągu arytmetycznego: a_n = a_k + (n − k)*r W tym zadaniu: r = 4, n = 10, k = 2, a₂ = 7 a₁₀ = 7 + (10 − 2)*4 = 39

M4ciek: −12 xD wybacz , ale nie jestem skupiony jak pisze na komputerze nie ma to jak na kartce.

Eta: Ok ...... tylko nie licz tak !... na maturze

M4ciek: No postaram sie

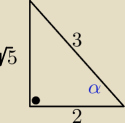
Eta: zad. 4/ dla kąta ostrego α

	2
cosα=
	3

b= 2 c= 3 to: a= √5

	a		√5
tgα=		=
	b		2

	5
tg2α=
	4

	5
2 +4*		= 2+5= 7
	4