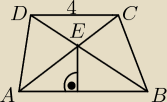
Czworkoąt ABCD na rysunku obok jest trapezem. Oblicz pola trójkątów ABE, DEC, AED, BCE.
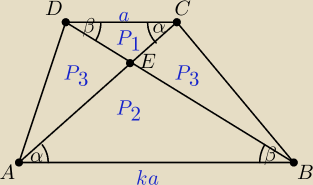ΔABE∼ΔCDE w skali k.
Jeśli pole trójkąta CDE jest równe P1, pole trójkąta ABE jest równe P2, pole trójkąta AED
i trójkąta BCE jest równe P3, to P2 = k2P1 i P3 = kP1.
Pole trapezu APCD jest równe PT = P1(k + 1)2
| 1 | k2 | k | ||||
P1 = | PT, P2 = | PT, P3 = | PT | |||
| (k + 1)2 | (k + 1)2 | (k + 1)2 |
