Proszę o wytłumaczenie zadania
dt(: W ostrosłupie czworokątnym prawidłowym ściana boczna jest nachylona do płaszczyzny podstawy pod
kątem 45 stopni. − Wyznacz kąt nachylenia krawędzi bocznej do płaszczyzny podsawy.
6 paź 21:08
TrolleY: Hm, jesteś nadal i zależy Ci na tym rozwiązaniu? Bo jak nie to nie będę się mordował z tym i z
rysunkami

Puki co wyszło mi tylko że sinα =
√3/3 (α to szukany kąt) a więc i tak nie wiem
jaką ten kąt ma miarę ale może Ci to coś da

6 paź 21:39
dt(: jestem
6 paź 21:41
TrolleY: To jak? Bawić się w to rysowanie itd?
6 paź 21:42
dt(: tak..

6 paź 21:42
TrolleY:
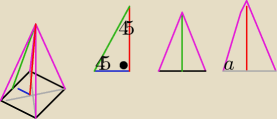
Mam nadzieję że coś tu widzisz

czarny − b
zielony − h
czerwony − H
niebieski − x = a/2
szary − y = a
√2
różowy − d
5
45st ma kąt zawarty między h i b stąd H = x = a/2, h =
√2/2a
później korzystasz z drugiego trójkąta, z pitagorasa możesz obliczyć
d=
√(a/2)2 + (√2a/2)2
d=
√3/4a2
d=
√3/2
z trzeciego trójkąta możesz obliczyć dowolną funkcję trygonometryczną tego kąta
6 paź 22:02
TrolleY: no i stąd mi wyszło sinα = √3/3, ew z tablic możesz znaleźć przybliżenie tego kąta
6 paź 22:04
dt(: dziękuję bardzo
6 paź 22:04
TrolleY: spoko

6 paź 22:07
Bogdan:
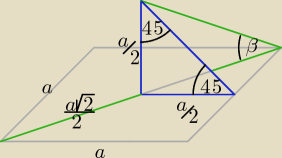
I sposób:
| | | | √2 | | √2 | |
tgβ = |
| * |
| = |
| ⇒ β = ... odczytujemy z tablic |
| | | | √2 | | 2 | |
II sposób:
W ostrosłupie prawidłowym n−kątnym między miarą kąta α nachylenia ściany bocznej do
płaszczyzny podstawy i miarą kąta β nachylenia krawędzi bocznej do płaszczyzny podstawy
| | π | | tgβ | |
zachodzizależność: cos |
| = |
| |
| | n | | tgα | |
| | π | | √2 | |
W tym przypadku: n = 4, cos |
| = cos45o = |
| , tgα = tg45o = 1 |
| | 4 | | 2 | |
| √2 | | tgβ | | √2 | |
| = |
| ⇒ tgβ = |
| |
| 2 | | 1 | | 2 | |
7 paź 00:33
 Puki co wyszło mi tylko że sinα = √3/3 (α to szukany kąt) a więc i tak nie wiem
jaką ten kąt ma miarę ale może Ci to coś da
Puki co wyszło mi tylko że sinα = √3/3 (α to szukany kąt) a więc i tak nie wiem
jaką ten kąt ma miarę ale może Ci to coś da 

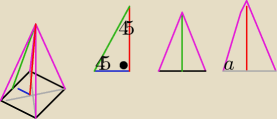 Mam nadzieję że coś tu widzisz
Mam nadzieję że coś tu widzisz  czarny − b
zielony − h
czerwony − H
niebieski − x = a/2
szary − y = a√2
różowy − d
5
45st ma kąt zawarty między h i b stąd H = x = a/2, h = √2/2a
później korzystasz z drugiego trójkąta, z pitagorasa możesz obliczyć
d= √(a/2)2 + (√2a/2)2
d= √3/4a2
d= √3/2
z trzeciego trójkąta możesz obliczyć dowolną funkcję trygonometryczną tego kąta
czarny − b
zielony − h
czerwony − H
niebieski − x = a/2
szary − y = a√2
różowy − d
5
45st ma kąt zawarty między h i b stąd H = x = a/2, h = √2/2a
później korzystasz z drugiego trójkąta, z pitagorasa możesz obliczyć
d= √(a/2)2 + (√2a/2)2
d= √3/4a2
d= √3/2
z trzeciego trójkąta możesz obliczyć dowolną funkcję trygonometryczną tego kąta

 I sposób:
I sposób: