Pomóżcie
xxx: Rozwiąż nierówność
(x2−4)|x3−1|>0
5 paź 23:01
xxx: Pierwszy nawias rozpisałem tak (x−2)(x+2), ale nie wiem co dalej
5 paź 23:03
M4ciek: (x−2)(x+2)(x3−1) > 0 v (x−2)(x+2)(−x3+1) < 0
5 paź 23:05
M4ciek: Chyba to nie tak powinno wygladac...
Spojrz kilka postow nizej Godziu Ci to napisal

5 paź 23:08
xxx: Dziękuję za pomoc, ale jak mam dalej postąpić z 2 nawiasów wyliczyłam że x=2 i x=−2 i nie wiem
co dalej
5 paź 23:08
xxx: Napisał mi, ale za bardzo nie rozumiem z czego to wynika. Dlaczego x należy do R. Nie rozumiem
5 paź 23:09
Jurek: |x3−1|>0 dla x≠1
x2−4>0 dla x∊(−∞;−2) V (2;+∞)
5 paź 23:10
Godzio:
|x3 − 1| > 0
wartość bezwzględna jest zawsze ≥ 0 w tym wypadku dla 1 jest równa zero więc to trzeba wywalić
5 paź 23:12
M4ciek: No x∊R\{1} dlatego , ze jezeli mamy wyrazenie pod wartoscia bezwzgledna to jest ono wieksze
badz rowne 0, a Twoja nierownosc ma byc wieksza od 0 wiec x moze byc dowolna liczba czyli
nalezy do R, poza 1 bo kiedy podstawimy za x cyfre 1 to otrzymamy 0 , a 0 nie jest wieksze od
0

5 paź 23:12
M4ciek: Godziu a nie moze byc tak jak napisalem? Czy to bez sensu?W sensie rozpisanie na 2 przypadki?
5 paź 23:13
Godzio: może być ale po pierwsze muszą być napisane przedziały na jakich to robisz a po drugie
nie trzeba zmieniać znaku nierówności, tylko zmieniasz opuszczając bezwzględność
5 paź 23:15
xxx: A ja mam właśnie rozpisać to na przypadki, a z tym mam spory problem
5 paź 23:18
M4ciek: Czyli (x−2)(x+2)(x
3−1) > 0 v (x−2)(x+2)(−x
3 +1) > 0
A przedzialy beda :
x∊(1;+
∞) v x∊(−
∞;1)

5 paź 23:19
Godzio: Teraz ok

5 paź 23:22
xxx: A 2 nie trzeba uwzględniać?
5 paź 23:23
M4ciek: Dobrze , ze tu trafilem teraz

a nie np. w kwietniu

5 paź 23:25
M4ciek: No teraz xxx wyznaczasz miejsca zerowe , zaznaczasz na osi i masz. Tak Godziu?
5 paź 23:27
xxx: czyli z 1 wyjdzie x=2 i x=−2 i x=1, czyli x=−2 będzie rozwiązaniem czy jak?
5 paź 23:30
M4ciek: Ehh rozwiazanie bedzie takie samo jak Godziu podal ,a wiec x∊(−∞;−2) ∪ (2;+∞)
5 paź 23:32
xxx: To ja juz nie rozumiem
5 paź 23:35
xxx: Jak mam zrobić poprawnie 1 przypadek
5 paź 23:40
xxx: z 1 mi wyszło x>2 i x>−2 i x>1
5 paź 23:50
xxx: Może mi to ktoś po kolei wytłumaczyc, chociaż na 1 przypadku, proszę
5 paź 23:51
Godzio: Dobra to tak na szybko
5 paź 23:52
xxx: Dziękuję bardzo

5 paź 23:54
Godzio:
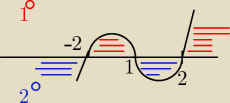
(x
2−4)|x
3−1|>0
x
3 − 1 > 0 ⇒ x > 1 ⇒ |x
3 − 1| = x
3 − 1
1o x ∊ (1,
∞)
(x
2 − 4)(x
3 − 1) > 0
(x − 2)(x + 2)(x − 1)(x
2 + x + 1) > 0
x ∊ (−2,1) ∪ (2,
∞) −−− rozwiązanie może należeć tylko do przedziału który badamy więc odpowiedź
do tego przypadku to: x ∊ (2,
∞)
x
3 − 1 < 0 ⇒ x < 1 ⇒ |x
3 − 1| = −x
3 + 1
2o x ∊ (−
∞,1)
(x
2 − 4)(−x
3 + 1) > 0
(x − 2)(x + 2)(x − 1)(x
2 + x + 1) < 0
x ∊ (−
∞,−2) ∪ (1,2) −− i znów rozwiązanie musi się zawierać w danym przedziale więc odpowiedź z
tego przedziału to: x ∊ (−
∞,−2)
Rozwiązanie to suma rozwiązań:
Odp: x ∊ (−
∞,−2) ∪ (2,
∞)
Dobranoc

5 paź 23:58
xxx: Dziękuję, jesteś wielki dobranoc
5 paź 23:59




 a nie np. w kwietniu
a nie np. w kwietniu 

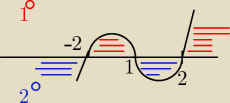 (x2−4)|x3−1|>0
x3 − 1 > 0 ⇒ x > 1 ⇒ |x3 − 1| = x3 − 1
1o x ∊ (1,∞)
(x2 − 4)(x3 − 1) > 0
(x − 2)(x + 2)(x − 1)(x2 + x + 1) > 0
x ∊ (−2,1) ∪ (2,∞) −−− rozwiązanie może należeć tylko do przedziału który badamy więc odpowiedź
do tego przypadku to: x ∊ (2,∞)
x3 − 1 < 0 ⇒ x < 1 ⇒ |x3 − 1| = −x3 + 1
2o x ∊ (−∞,1)
(x2 − 4)(−x3 + 1) > 0
(x − 2)(x + 2)(x − 1)(x2 + x + 1) < 0
x ∊ (−∞,−2) ∪ (1,2) −− i znów rozwiązanie musi się zawierać w danym przedziale więc odpowiedź z
tego przedziału to: x ∊ (−∞,−2)
Rozwiązanie to suma rozwiązań:
Odp: x ∊ (−∞,−2) ∪ (2,∞)
Dobranoc
(x2−4)|x3−1|>0
x3 − 1 > 0 ⇒ x > 1 ⇒ |x3 − 1| = x3 − 1
1o x ∊ (1,∞)
(x2 − 4)(x3 − 1) > 0
(x − 2)(x + 2)(x − 1)(x2 + x + 1) > 0
x ∊ (−2,1) ∪ (2,∞) −−− rozwiązanie może należeć tylko do przedziału który badamy więc odpowiedź
do tego przypadku to: x ∊ (2,∞)
x3 − 1 < 0 ⇒ x < 1 ⇒ |x3 − 1| = −x3 + 1
2o x ∊ (−∞,1)
(x2 − 4)(−x3 + 1) > 0
(x − 2)(x + 2)(x − 1)(x2 + x + 1) < 0
x ∊ (−∞,−2) ∪ (1,2) −− i znów rozwiązanie musi się zawierać w danym przedziale więc odpowiedź z
tego przedziału to: x ∊ (−∞,−2)
Rozwiązanie to suma rozwiązań:
Odp: x ∊ (−∞,−2) ∪ (2,∞)
Dobranoc 