3 zadanka
ktoś;p: 1. Wyznacz równanie symetralnej odcinka AB, korzystając ze wzoru na odległość między punktami,
A(1,8), B(5,4).
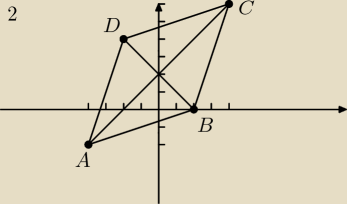
2. Pole rombu jest równe 32. Wyznacz współrzędne punktów B i D, jeśli A(−4,−2) i C(4,6)
3. Punkty A(4,2) i B(1,6) są wierzchołkami równoległoboku ABCD, którego przekątne przecinają
się w punkcie (0,3). Wyznacz równanie symetralnej boku CD.
Proszę o wskazówki, bo ja zawsze coś pochrzanie i nie chce wyjść
5 paź 22:28
M4ciek: Pokaz jak robisz

5 paź 23:20
ktoś;p: o to chodzi,że nie wiem jak zacząć

narysowałam sobie odcinek i symetralną i jestem w lesie

5 paź 23:22
Godzio:
Powinienem spać już od 1 h ale niestety nie udało mi się zasnąć więc spróbuje ponownie za 10
min, i w tym momencie zostałeś wybrany na ostatnie zadanie na dziś

czekaj 10 min,
dostaniesz zadanie a ja pójdę spać pasi

?
5 paź 23:26
ktoś;p: yhym

5 paź 23:26
ktoś;p: też zaraz muszę iść,więc te dwa dokończę jutro

a powiedź mi tak z czystej ciekawości skąd
jesteś


5 paź 23:30
M4ciek: A co chcesz mu czekolade wyslac

? Powiedz skad Ty

5 paź 23:31
ktoś;p: czekoladę może nie

nie wiadomo czy lubi

ja jestem spod Krakowa

5 paź 23:33
M4ciek: Na pewno lubi

To masz daleko

5 paź 23:34
ktoś;p: daleko do Ciebie czy do Godzia


5 paź 23:36
M4ciek: Tu i tu , do mnie blizej

5 paź 23:37
M4ciek: Lece spac bo trzeba jakos wstac

Dobranoc
5 paź 23:38
ktoś;p: szkoda

5 paź 23:39
ktoś;p: Dobranoc

5 paź 23:39
Godzio:
1. Symetralna do prosta przechodząca przez środek odcinka i dzieląca go na pół, więc:
W pierwszym kroku policzę prostą AB i środek odcinka AB:
A(1,8) B(5,4)
8 = a + b
4 = 5a + b −
−−−−−−−−−−−−−−
4 = −4a ⇒ a = −1
b = 9
y
AB = −x + 9
| | 1 + 5 | | 8 + 4 | |
SAB = ( |
| , |
| ) = (3,6) |
| | 2 | | 2 | |
S
AB(3,6)
Skoro prostopadła to jej współczynnik możemy obliczyć tak: a
1 * a = −1 ⇒ a
1 = 1
Mając punkt i współczynnik kierunkowy można obliczyć b:
6 = 1 * 3 + b ⇒ b = 3
Zatem równanie prostej symetralnej to: y = x + 3
2.
Pole rombu można obliczyć ze wzoru:
| | e * f | |
P = |
| , e,f − przekątne rombu które przecinają się pod kątem prostym |
| | 2 | |
e = |AC|
f = |BD|
A(−4,−2) C(4,6) ⇒ |AC| =
√(4 + 4)2 + (6 + 2)2 =
√82 + 82 =
√2 * 82 = 8
√2
| | 8√2 * f | |
P = |
| = 32 ⇒ √2f = 8 ⇒ f = 4√2 |
| | 2 | |
Środek AC (punkt przecięcia się przekątnych) :
S
AC(0,2)
Prosta AC:
−2 = −4a + b
6 = 4a + b −
−−−−−−−−−−−−−
−8 = − 8a
a = 1 ⇒ b = 2
y
AC = x + 2
Prosta prostopadła do AC przechodząca przez punkty B i D:
y = −x + 2
| | 1 | |
wiemy że odległość SB = SD = |
| f = 2√2 więc |
| | 2 | |
|SB| = 2
√2
√(x − 0)2 + (y − 2)2 = 2
√2 /
2 i
y = −x + 2
x
2 + x
2 = 8
2x
2 = 8
x
2 = 4
x = 2 v x = −2
y = 0 v y = 4
B(2,0) D(−2,4)
3. za chwilkę
5 paź 23:39
Godzio:
Ja z Wrocławia jestem

Już trzecie zrobię więc nie uciekaj

5 paź 23:40
ktoś;p: dobrze

5 paź 23:41
Godzio:
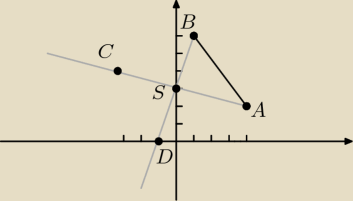
3. Punkty A(4,2) i B(1,6) są wierzchołkami równoległoboku ABCD, którego przekątne przecinają
się w punkcie (0,3). Wyznacz równanie symetralnej boku CD. Proszę o wskazówki, bo ja zawsze
coś pochrzanie i nie chce wyjść
A(4,2) B(1,6) S(0,3)
Przekątna BD:
Prosta przechodzi przez B i S więc można znaleźć jej równanie:
S(0,3) ⇒ b = 3
6 = a + 3
a = 3
y
BD = 3x + 3
długość |SB| musi być równa |SD| więc:
|SB| =
√10
|SD| =
√x2 + (y − 3)2 i y = 3x + 3
√10 =
√x2 + 9x2 /
2
10 = 10x
2
x
2 = 1
x = 1 v x = − 1 ⇒ y = 6 v y = 0 D(−1,0)
Prosta DC jest równoległa do prostej AB więc:
y
AB:
2 = 4a + b
6 = a + b −
−−−−−−−−−−−−−
−4 = 3a
żeby obliczyć C użyję prostej AS:
2 = 4a + 3
−1 = 4a
punkt przecięcia prostej y
CD i y
AS da punkt C
| | 1 | | 4 | | 4 | |
− |
| x + 3 = − |
| x − |
| /*12 |
| | 4 | | 3 | | 3 | |
−3x + 36 = −16x − 16
13x = −52
x = −4 ⇒ y = 4
Do symetralnej potrzebuje jeszcze środka CD:
| | 4 | | 4 | |
C(−4,4) D(−1,0) yCD = − |
| x − |
| |
| | 3 | | 3 | |
S
CD(−2,5 ; 2)
| | 3 | | 23 | |
Równanie symetralnej: y = |
| x + |
| |
| | 4 | | 8 | |
Jak jest gdzieś błąd to sobie znajdziesz i poprawisz
Dobranoc

5 paź 23:52
ktoś;p: Dziękuję bardzo

5 paź 23:53
ktoś;p: Dobranoc

5 paź 23:54
lalal: tam powinno być b = 31/8 a równanie symetralnej powinno być równe y=3/4x + 31/8 czyli y=3/4x +
3i7/8
25 maj 19:24
agata: czemu tam jest napisane ze |SB|=√10 ? skad to sie wzielo?
7 paź 19:55
Crissu: stąd:
S (0;3) B (1;6)
S (x1;y1 B (x2;y2)
|SB|= √(x2−x1)2+(y2−y1)2
|SB|= √(1−0)2+(6−3)2=√1+9=√10
9 paź 23:42

 narysowałam sobie odcinek i symetralną i jestem w lesie
narysowałam sobie odcinek i symetralną i jestem w lesie
 czekaj 10 min,
dostaniesz zadanie a ja pójdę spać pasi
czekaj 10 min,
dostaniesz zadanie a ja pójdę spać pasi  ?
?

 a powiedź mi tak z czystej ciekawości skąd
jesteś
a powiedź mi tak z czystej ciekawości skąd
jesteś

 ? Powiedz skad Ty
? Powiedz skad Ty 
 nie wiadomo czy lubi
nie wiadomo czy lubi ja jestem spod Krakowa
ja jestem spod Krakowa
 To masz daleko
To masz daleko 



 Dobranoc
Dobranoc


 1. Symetralna do prosta przechodząca przez środek odcinka i dzieląca go na pół, więc:
W pierwszym kroku policzę prostą AB i środek odcinka AB:
A(1,8) B(5,4)
8 = a + b
4 = 5a + b −
−−−−−−−−−−−−−−
4 = −4a ⇒ a = −1
b = 9
yAB = −x + 9
1. Symetralna do prosta przechodząca przez środek odcinka i dzieląca go na pół, więc:
W pierwszym kroku policzę prostą AB i środek odcinka AB:
A(1,8) B(5,4)
8 = a + b
4 = 5a + b −
−−−−−−−−−−−−−−
4 = −4a ⇒ a = −1
b = 9
yAB = −x + 9
 Już trzecie zrobię więc nie uciekaj
Już trzecie zrobię więc nie uciekaj 

 3. Punkty A(4,2) i B(1,6) są wierzchołkami równoległoboku ABCD, którego przekątne przecinają
się w punkcie (0,3). Wyznacz równanie symetralnej boku CD. Proszę o wskazówki, bo ja zawsze
coś pochrzanie i nie chce wyjść
A(4,2) B(1,6) S(0,3)
Przekątna BD:
Prosta przechodzi przez B i S więc można znaleźć jej równanie:
S(0,3) ⇒ b = 3
6 = a + 3
a = 3
yBD = 3x + 3
długość |SB| musi być równa |SD| więc:
|SB| = √10
|SD| = √x2 + (y − 3)2 i y = 3x + 3
√10 = √x2 + 9x2 /2
10 = 10x2
x2 = 1
x = 1 v x = − 1 ⇒ y = 6 v y = 0 D(−1,0)
Prosta DC jest równoległa do prostej AB więc:
yAB:
2 = 4a + b
6 = a + b −
−−−−−−−−−−−−−
−4 = 3a
3. Punkty A(4,2) i B(1,6) są wierzchołkami równoległoboku ABCD, którego przekątne przecinają
się w punkcie (0,3). Wyznacz równanie symetralnej boku CD. Proszę o wskazówki, bo ja zawsze
coś pochrzanie i nie chce wyjść
A(4,2) B(1,6) S(0,3)
Przekątna BD:
Prosta przechodzi przez B i S więc można znaleźć jej równanie:
S(0,3) ⇒ b = 3
6 = a + 3
a = 3
yBD = 3x + 3
długość |SB| musi być równa |SD| więc:
|SB| = √10
|SD| = √x2 + (y − 3)2 i y = 3x + 3
√10 = √x2 + 9x2 /2
10 = 10x2
x2 = 1
x = 1 v x = − 1 ⇒ y = 6 v y = 0 D(−1,0)
Prosta DC jest równoległa do prostej AB więc:
yAB:
2 = 4a + b
6 = a + b −
−−−−−−−−−−−−−
−4 = 3a


